 por jamiel » Qui Abr 28, 2011 13:11
por jamiel » Qui Abr 28, 2011 13:11
Esboce o gráfico das funções dando o domínio e a imagem de cada uma delas.
a) | x + 2 | = 0
x + 2 = 0
x = -2
Eu teria um gráfico com y=2 e x=-2. Espelhando a parte da função quando negativa, -x -2 .... -x = 2 ... x = -2. Com isso, uma reta de y=2 até x=-2 e x=-2 até -2?x .... Um "V", melhor dizendo. Minha dúvida é seguinte, neste gráfico o x=-2 é o valor do meio, que divide o, onde as duas retas partem, mas em direções opostas. O domínio seria "D=R" e a imagem seria "Im=R+". No meu entender, eu teria um limíte, que seria entre x=-4 e 0, estaria certo ou neste gráfico eu poderia trabalhar com qualquer valor na reta x não e positivo?
b) |x² + 2x - 3|
Se alguém puder comentar algo sobre essa do segundo grau, agradeço também. Como seria comportamento dessa parábola com valores atribuídos a "x"?
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por carlosalesouza » Seg Mai 02, 2011 00:09
por carlosalesouza » Seg Mai 02, 2011 00:09
a)
Na verdade, observemos o seguinte, sendo uma função modular,

, então, podemos representá-la da seguinte forma:
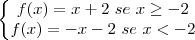
A sua demonstração y=2 até x=-2, na verdade, originaria uma reta constante, paralela ao eixo x...
Assim, o ponto de encontro das duas retas será (-2,0)
f(-1) = |-1+2|=1
f(-2) = |-2+2|=0
f(-3) = |-3+2|=|-1|=1
Ok?
b)
Primeiro, vamos fatorar:
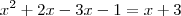
, logo:
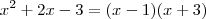
Portanto:
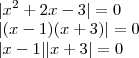
Aqui já encontramos as raízes:
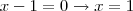
e

O gráfico terá o formato de um W e seus dois limites inferiores tocarão o eixo x, com y=0, nos pontos x=-3 e x=1
Entre esses valores de x, o gráfico será uma parábola e depois fora desse intervalo, duas retas simétricas.
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por jamiel » Seg Mai 02, 2011 02:33
por jamiel » Seg Mai 02, 2011 02:33
Obrigado!
Me custa assimilar esse assunto, um pouco.
f(-1) = |-1+2|=1
f(-2) = |-2+2|=0
f(-3) = |-3+2|=|-1|=1
Digamos q eu coloque f(1), f(2) e f(3). Isso estaria correto? Minha dúvida, basicamente, é essa. Eu posso trabalhar com qualquer valor de x
Por exemplo:
|x + 2| = 1
x = 1 -2
x = -1
e
-|x + 2| = 1
-x -2 = 1
-x = 1 +2
-x = 3
x = -3
Para o valor de y=1, por exemplo, eu tenho valores simétricos. Neste caso, (-3;1) e (-1;1). O valor "-2" estaria entre -3 e -1. Com isso, esses dois últimos estariam equidistantes, correto?
Obrigado mais uma vez!
É, justamente, essa simetria q a função modular busca?
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por carlosalesouza » Seg Mai 02, 2011 21:32
por carlosalesouza » Seg Mai 02, 2011 21:32
Rs... é mais ou menos por aí...
A questão da função modular é que ela não aceita valores negativos na imagem, mas o domínio aceita qualquer valor. Assim, podemos escrever a função de formas diferentes para ilustrá-la melhor.
O comportamento dela vai depender de seu grau. Como podemos ver pelos exemplos utilizados, a função modular de 1º grau apresenta gráfico em V, a de 2º forma um W, a de 3º (essa não temos aqui) formará duas curvas que partem do ponto y=0, mas que não apresentam qualquer simetria, ou seja, a função modular não é necessariamente simétrica. Sua característica principal é que o ponto (ou pontos) y=0 divide a função em segmentos, que podem ser definidos por funções condicionais.
Explicando melhor, se f(x) < 0 para um x qualquer, então |f(x)| = - f(x)
Foi falha minha, mas o gráfico da segunda função fica assim:
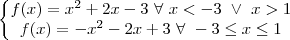
Traduzindo,
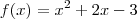
para todo x menor que -3 ou x maior que 1 (pois esses valores de x retornam y positivo) e
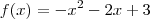
para todo x de -3 a 1 (pois esses valores de x retornam y negativo, sendo necessário inverter o sinal da função)...
Obviamente, existem funções que não apresentam imagem negativa... nestes casos, o módulo dessas funções não fará a mínima diferença... rs
Então, resumidamente, para traçar o gráfico de uma função modular, precisamos encontrar o domínio e a imagem da função contida dentro do módulo e verificar qual intervalo de D-->Im onde y>=0 e inverter o sinal da função para valores de x fora desse intervalo, traçamos e combinamos os gráfifcos das duas funções para encontrar o gráfico da função modular.
Espero ter ajudado... se surgiu mais alguma dúvida, pode perguntar, que estamos aqui pra isso... rs
Um abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por jamiel » Ter Mai 03, 2011 00:28
por jamiel » Ter Mai 03, 2011 00:28
Bacana sua explicação. Obrigado, mesmo.
Agora, outro ponto interessante é o valor q desloca o gráfico, por exemplo: |x + ''x| -5 = f(x).
Vlw mesmo ...
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por jamiel » Qua Mai 04, 2011 02:29
por jamiel » Qua Mai 04, 2011 02:29
Essa foi esquentar meu crânio!
|x-3| + 4x = 7
De início, se o 4x fosse apenas 4, deslocaria o gráfico do modulo. Porém, 4x é uma reta em diagonal passando por zero. Logo, o deslocamento estaria entre 4 e 7. Confesso q não consegui compreender.
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por LuizAquino » Qua Mai 04, 2011 11:04
por LuizAquino » Qua Mai 04, 2011 11:04
Eu recomendo que você assista as vídeo-aulas do canal do Nerckie no YouTube. Procure pela vídeo-aula "Matemática - Aula 26 - Função Modular". Elas estão divididas em 5 partes. O endereço do canal é:
http://www.youtube.com/nerckie
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por jamiel » Qua Mai 04, 2011 12:01
por jamiel » Qua Mai 04, 2011 12:01
Vlw Luiz!
Eu assisto, sempre q posso, as video-aulas dele. Confesso q falta assistir os outros vídeos de função modular, assisti os dois primeiros, eu acho.
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por carlosalesouza » Qua Mai 04, 2011 15:26
por carlosalesouza » Qua Mai 04, 2011 15:26
Pois é... o módulo só vai afetar o que está dentro do módulo, pois se f(x)<0, então |f(x)|=-f(x)
Nesse caso, f(x) = |x-3|+4x = 7 fica:
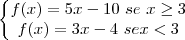
Observe que 5(3)-10 = 5 e 3(3)-4 = 5.
Logo, o ponto de partida das duas retas será (3,5)
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por jamiel » Qua Mai 04, 2011 16:17
por jamiel » Qua Mai 04, 2011 16:17
Ok, eu fiz dessa maneira, mas o gráfico quando eu coloquei no programa "Wolfram(esse programa é muito difícil, nem sei por onde começar! rssr)" e no Winplot ficou um gráfico meio esquisito!
Mas vlw pela dica, de qualquer forma!
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por jamiel » Qua Mai 04, 2011 16:25
por jamiel » Qua Mai 04, 2011 16:25
Ah, outra, o conjunto Verdade é x={4/3}!
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por carlosalesouza » Qua Mai 04, 2011 21:04
por carlosalesouza » Qua Mai 04, 2011 21:04
Pra criar gráficos, eu recomendo o graphmatica... é simples e fácil de entender... tem uma barra de endereço, onde voce digita a equação de forma linear, tipo y=|x+3|+4x-7
E ele vai traçar o gráfico pra voce... rs
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por LuizAquino » Qua Mai 04, 2011 21:25
por LuizAquino » Qua Mai 04, 2011 21:25
Um ótimo programa para traçar gráficos, realizar construções geométricas e muito mais é o GeoGebra. O página oficial do programa é:
http://www.geogebra.orgEm meu canal no YouTube há um curso ensinando a usar esse programa. O endereço é:
http://www.youtube.com/LCMAquino
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por jamiel » Qua Mai 04, 2011 21:50
por jamiel » Qua Mai 04, 2011 21:50
Obrigado mais uma vez. Eu fiz o gráfico em dois programas diferentes, mais, usei a barra de navegação da Wolfram online q mostra até equação balanceada de química rsrsr
O problema é q não estou entendo o gráfico. As retas de |x-3| formam um V, ok, mas com toda a equação resolvida, a reta do lado direito, após o 3, continua no mesmo sentido, a do lado direito parece descer um pouco(inclina mais ainda para a esquerda) e a origem do gráfico(o V q se encontra em x=3) sobe 14 unidades em y. Muito louca essa equação! rsrsr
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por jamiel » Qui Mai 05, 2011 02:23
por jamiel » Qui Mai 05, 2011 02:23
Essa equação tá me dando trabalho!
Respirando fundo! Deixa ver se eu entendi:
|x-3|+4x=7
Primeiro caso:
|x-3|?0
x - 3 + 4x = 7
5x -10, se |x-3|?0
segundo caso:
|x-3|<0
-x + 3 + 4x = 7
3x -4, se |x-3|<0
Até aí, tudo bem!
5x -10, se |x-3|?0 e 3x -4, se |x-3|<0
*Digamos q eu plote as duas retas dessas duas equações -->
5x - 10 e 3x - 4
*Posso ousar----- 5x-10=3x-4 --> 2x = 6 --> x = 3. Em um dado momento elas passam pelo ponto x=3
5•3 -10 = 5 e 3•3 -4 = 5, ambas tem y=5 em comum.
*Com todo esse arranjo, igualando todos os valores iniciais numa só situação(lado da equação), o 7, o 4x e |x-3|, restam os pontos comuns. Se há algum, é claro!
*Com toda essa mistura de valores o x fica responsável pelo deslocamento do |x-3|. Logo, 5•3 -10 = 5 e 3•3 -4 = 5, o modulo começa no x=3 na altura y=5.
*Voltando com as restrições anteriormente determinadas, subentende-se que 5x - 10 só é verdadeiro do ponto x=3 em diante e 3x -4 até x<3.
*Finalizando:
É como se criasse um novo "modulo", um reta final "espelho", como? Unindo a parte verdadeira da reta 5x-10 e 3x-4, ficando assim, uma reta "torta". E o contrário também, se invertermos as restrições a reta espelho final é a mesma, porém, contrária.
Eu acho q consegui entender, com muito sacrifício, mas obtive isso. Brigadão pelos toques Aquino. Baixei o programa q vc me recomendou e irei usá-lo amanhã mesmo. Ah, e ver seus vídeos no youtube.
Atualmente, estou no primeiro em Lic. Química e iniciarei a escola técnica IFPE(antigo CEFET-PE) no curso de Mecânica no segundo semestre. Sinto um grande entusiasmo pela matemática, de uns tempos para cá, cogitando a possibilidade, mais à frente, de cursar engenharia. Qualquer conselho seria bem-vindo acerca "engenharia", sei, por alto, q é muito puxado esse curso!
vlw ....
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por carlosalesouza » Qui Mai 05, 2011 08:44
por carlosalesouza » Qui Mai 05, 2011 08:44
Ahghahaha... calma... calma... rs
Como eu disse antes, a gente não precisa se preocupar com a simetria ou o formato da função modular em V.
A propriedade relevante, aqui, da função modular, é que ela divide a função em duas funções, de acordo com o valor de x.
Assim, quando traçamos as funções condicionais no plano cartesiano, devemos lembrar que se u(x) para x>=a e v(x) para x < a, então devemos traçar a função u(x) somente do ponto (a,y(a)) para a direita e a função v(x) para os valores de x à esquerda do ponto x=a.
Esta função realmente resultará em duas retas concorrentes com inclinação bem próxima, tendo como vértice o ponto (3,5)...
Mais uma vez, não esquenta a cabeça com o gráfico da função modular... hehehehe
Pra tirar a prova, você pode tanto pedir para o programa de sua preferência (e o geogebra é realmente imbatível, em todos os aspectos) traças as duas funções resultantes da função modular e analisar a área de interesse de cada uma delas ou escrever a função do jeito que voce tem ali:
y=|x-3|+4x-7
Que ele vai traçar já a função modular bonitinha... heheheheh
Um abraço...
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por LuizAquino » Qui Mai 05, 2011 09:04
por LuizAquino » Qui Mai 05, 2011 09:04
Vamos deixar algo bem claro: o texto "|x - 3| + 4x = 7" representa uma
equação e não uma função.
Se tivéssemos duas variáveis nessa equação, aí sim poderíamos enxergá-la como uma função. Por exemplo, se tivéssemos: |x - 3| + 4x = 7 + 2y. Nesse caso, poderíamos dizer que temos:
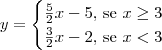
Enxergando y como uma função de x, ou seja, y = f(x), aí poderíamos traçar o gráfico dessa função.
Por outro lado, o que temos originalmente é uma
equação com apenas uma incógnita. Isso significa que você deve encontrar os valores da incógnita x que tornam a equação |x - 3| + 4x = 7 verdadeira.
Nesse caso, temos que:
|x - 3| + 4x = 7
|x - 3| = 7 - 4x
Usando a definição de módulo, isso gera duas equações:
(a) x - 3 = 7 - 4x, se x >= 3.
(b) -(x - 3) = 7 - 4x, se x < 3.
A equação (a) tem solução x = 2. Mas, como devemos ter x >= 3, essa solução não é válida.
Já a equação (b) tem solução x=4/3. Note que esse valor de x é tal que x < 3.
Portanto, a solução da equação original é S = {4/3}. Para testar a solução, substitua x por esse valor na equação original e você verá que a equação fica verdadeira.
Podemos ainda ter mais outra interpretação. Dada a equação |x - 3| + 4x = 7, podemos escrever |x - 3| + 4x - 7 = 0. Se forçarmos um pouco a barra e enxergarmos o primeiro membro dessa equação como se fosse uma função de x, então temos a equação f(x)=0. Desse modo, geometricamente falando, para resolver a equação original temos que determinar a interseção do gráfico de f(x) com o eixo x.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por carlosalesouza » Qui Mai 05, 2011 09:35
por carlosalesouza » Qui Mai 05, 2011 09:35
Eu acho que é assunto encerrado então... heheheheh
Um abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por jamiel » Qui Mai 05, 2011 14:08
por jamiel » Qui Mai 05, 2011 14:08
Aquino, eu acho q entendi melhor agora. Isso não é uma função modular, mas uma equação modular, tanto é q o conjunto verdade é v={4/3}. Eu acho q me equivoquei, mais, me compliquei tanto. Obrigado a todos mais uma vez.
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função modular - Dúvida
por Danilo » Dom Mar 10, 2013 15:50
- 1 Respostas
- 1521 Exibições
- Última mensagem por e8group

Dom Mar 10, 2013 16:49
Funções
-
- Dúvida (derivada e função modular)
 por Man Utd » Sáb Jun 15, 2013 11:03
por Man Utd » Sáb Jun 15, 2013 11:03
- 5 Respostas
- 7665 Exibições
- Última mensagem por LuizAquino

Dom Jun 16, 2013 11:24
Cálculo: Limites, Derivadas e Integrais
-
- [Função modular] Dúvida com relação a raízes
por exburro » Sáb Mar 31, 2012 01:23
- 1 Respostas
- 2587 Exibições
- Última mensagem por LuizAquino

Sex Abr 06, 2012 12:40
Funções
-
- [inequação modular] DÚVIDA SIMPLES EM INEQUAÇÃO MODULAR
por brunocunha2008 » Sex Set 13, 2013 22:37
- 1 Respostas
- 7385 Exibições
- Última mensagem por Rafael Henrique

Qui Jan 03, 2019 14:39
Inequações
-
- Inequação Modular (Dúvida)
 por renanrdaros » Ter Mar 22, 2011 23:33
por renanrdaros » Ter Mar 22, 2011 23:33
- 13 Respostas
- 11530 Exibições
- Última mensagem por renanrdaros

Qua Mar 23, 2011 17:36
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?

O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois

2°) Admitamos que

, seja verdadeira:

(hipótese da indução)
e provemos que

Temos: (Nessa parte)

Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para

.




Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:

, certo? O autor começou do primeiro membro:

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

Que é outra verdade. Agora, com certeza:

Agora, como

é

a

, e este por sua vez é sempre

que

, logo:

Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 , então, podemos representá-la da seguinte forma:
, então, podemos representá-la da seguinte forma: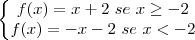
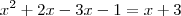 , logo:
, logo: 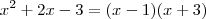
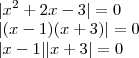
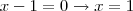 e
e 


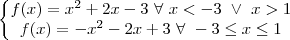
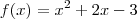 para todo x menor que -3 ou x maior que 1 (pois esses valores de x retornam y positivo) e
para todo x menor que -3 ou x maior que 1 (pois esses valores de x retornam y positivo) e 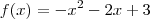 para todo x de -3 a 1 (pois esses valores de x retornam y negativo, sendo necessário inverter o sinal da função)...
para todo x de -3 a 1 (pois esses valores de x retornam y negativo, sendo necessário inverter o sinal da função)...




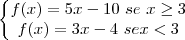








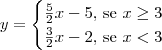





 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 seja verdadeiro, e pretendemos provar que também é verdadeiro para
seja verdadeiro, e pretendemos provar que também é verdadeiro para  .
.



 , certo? O autor começou do primeiro membro:
, certo? O autor começou do primeiro membro:


 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo:
