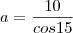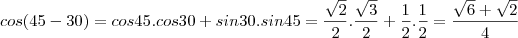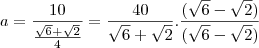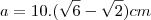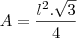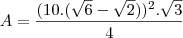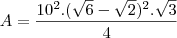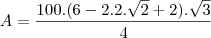por Mi_chelle » Qua Mai 04, 2011 20:17
por Mi_chelle » Qua Mai 04, 2011 20:17
Não estou conseguindo resolver a seguinte questão:
(Unicamp) Sejam A,B,C e D os vértices de um quadrado de lado a= 10cm; Sejam ainda E e F pontos nos lados AD e DC respectivamente, de modo que BEF seja um triângulo equilátero.
a)Qual o comprimento do lado desse triângulo.
b) Calcule a área do mesmo.
Tentativa:
a)Inicialmente fiz as seguintes deduçoes:
AE=CF=y
DE=DF=Z
m seria a altura do triângulo, então m=
![\frac{x.\sqrt[]{3}}{2} \frac{x.\sqrt[]{3}}{2}](/latexrender/pictures/33825d607b3790da3c00bdeebfdaa56e.png)
A soma das áreas dos triângulos ABE, DEF, BCF E BEF é igual a 100cm²
Então,
![[tex]\frac{10.y}{2}+\frac{{z}^{2}}{2}+\frac{10.y}{2}+\frac{x.m}{2} [tex]\frac{10.y}{2}+\frac{{z}^{2}}{2}+\frac{10.y}{2}+\frac{x.m}{2}](/latexrender/pictures/7f97c5f49ec9881a8e090c612dc9e3ca.png)
=100.
Resolvendo essa equação, cheguei ao resultado:
x²=
![\frac{100\sqrt[]{3}}{3} \frac{100\sqrt[]{3}}{3}](/latexrender/pictures/ee4c9b8034907608a9c548b7f48e6877.png)
.
Porém no gabarito a resposta é:
a)10(
![\sqrt[]{6}-\sqrt[]{2} \sqrt[]{6}-\sqrt[]{2}](/latexrender/pictures/54a31b3e31784da69f4c24dfb7baa5a3.png)
)cm.
b)100(2
![\sqrt[]{3}-3) \sqrt[]{3}-3)](/latexrender/pictures/122d6d8440180c126b70880235409ad7.png)
cm².
Onde foi que eu errei?
-
Mi_chelle
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Seg Mar 28, 2011 17:35
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Química
- Andamento: formado
 por FilipeCaceres » Qua Mai 04, 2011 21:19
por FilipeCaceres » Qua Mai 04, 2011 21:19
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Mi_chelle » Qui Mai 05, 2011 17:28
por Mi_chelle » Qui Mai 05, 2011 17:28
Obrigada pela ajuda.
Não conhecia essa fórmula para encontrar a área de triângulos equiláteros. Ajuda bastante.
Obrigada novamente.
-
Mi_chelle
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Seg Mar 28, 2011 17:35
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Química
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Razão da área do triângulo para a área do quadrilátero]
 por Mayra Luna » Sex Nov 23, 2012 20:17
por Mayra Luna » Sex Nov 23, 2012 20:17
- 2 Respostas
- 4414 Exibições
- Última mensagem por Mayra Luna

Ter Nov 27, 2012 14:53
Geometria Plana
-
- [Área] Área de triangulo e trapézio
 por smlspirit » Qui Jul 19, 2012 20:07
por smlspirit » Qui Jul 19, 2012 20:07
- 1 Respostas
- 2996 Exibições
- Última mensagem por e8group

Qui Jul 19, 2012 20:57
Geometria Plana
-
- Área do Triângulo
por Padoan » Qui Fev 11, 2010 18:36
- 6 Respostas
- 8369 Exibições
- Última mensagem por MarceloFantini

Sex Fev 12, 2010 13:42
Geometria Plana
-
- Área do Triângulo
por Cleyson007 » Sex Mai 14, 2010 13:07
- 1 Respostas
- 2325 Exibições
- Última mensagem por Douglasm

Sex Mai 14, 2010 13:38
Geometria Analítica
-
- Área do Triângulo
por valeuleo » Ter Abr 05, 2011 11:25
- 1 Respostas
- 2692 Exibições
- Última mensagem por LuizAquino

Ter Abr 05, 2011 11:42
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{x.\sqrt[]{3}}{2} \frac{x.\sqrt[]{3}}{2}](/latexrender/pictures/33825d607b3790da3c00bdeebfdaa56e.png)
![[tex]\frac{10.y}{2}+\frac{{z}^{2}}{2}+\frac{10.y}{2}+\frac{x.m}{2} [tex]\frac{10.y}{2}+\frac{{z}^{2}}{2}+\frac{10.y}{2}+\frac{x.m}{2}](/latexrender/pictures/7f97c5f49ec9881a8e090c612dc9e3ca.png) =100.
=100.![\frac{100\sqrt[]{3}}{3} \frac{100\sqrt[]{3}}{3}](/latexrender/pictures/ee4c9b8034907608a9c548b7f48e6877.png) .
.![\sqrt[]{6}-\sqrt[]{2} \sqrt[]{6}-\sqrt[]{2}](/latexrender/pictures/54a31b3e31784da69f4c24dfb7baa5a3.png) )cm.
)cm.![\sqrt[]{3}-3) \sqrt[]{3}-3)](/latexrender/pictures/122d6d8440180c126b70880235409ad7.png) cm².
cm².

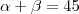
 corresponde a bissetriz do triângulo
corresponde a bissetriz do triângulo  , portanto
, portanto