 por escova » Sáb Abr 30, 2011 01:54
por escova » Sáb Abr 30, 2011 01:54
boa noite, es a dita cuja
'em meados de 2007 foram desmatados 11532km² ja em meados de 2008 foram 11968km² , com base nisso pode-se afirmar que de meados de 2007 a meados de 2008 o desmatamento teve um aumento aproximadamente de:
2,4% / 3,8% / 4,8% / 5,0% / 6,2% --- gabarito marca 3,8%
eu achei 3,78..% sera q a banca aproximou o valor para 3,8 na resposta?... prova A pmerj 2009
-
escova
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Abr 29, 2011 00:39
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: eletronica
- Andamento: formado
 por FilipeCaceres » Sáb Abr 30, 2011 02:09
por FilipeCaceres » Sáb Abr 30, 2011 02:09
Regra de Três



Ou seja, teve um aumento de

%
Portanto, o aumento foi de
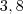
%
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por luizeduardo » Dom Mai 01, 2011 19:43
por luizeduardo » Dom Mai 01, 2011 19:43
Tenho uma relação que utilizo bastante para resolver questões semelhantes a esta:
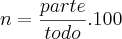
11 968 - 11 532 = 436 (parte aumentada)
11 532 (todo - do qual a porcentagem foi aplicada)

%
Espero ter ajudado e complementado a resposta do Filipe.
Luiz Eduardo
-
luizeduardo
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Abr 24, 2011 12:49
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por FilipeCaceres » Dom Mai 01, 2011 20:21
por FilipeCaceres » Dom Mai 01, 2011 20:21
Para quem não esta muito habituado a resolver este tipo de questão acredito que a melhor forma seja fazer por regra de três mesmo, pois a pessoa pode se perder quem é a parte ou quem é o todo.
Abraço à todos.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão de porcentagem
por LuizCarlos » Seg Abr 16, 2012 18:50
- 1 Respostas
- 1567 Exibições
- Última mensagem por DanielFerreira

Qua Abr 18, 2012 22:30
Álgebra Elementar
-
- [porcentagem] Questão de prova
por maryhelbling » Sex Jul 11, 2008 11:21
- 1 Respostas
- 3415 Exibições
- Última mensagem por admin

Sex Jul 11, 2008 11:32
Tópicos sem Interação (leia as regras)
-
- Porcentagem questao de concurso
por RENATO 7 » Dom Mar 20, 2011 21:08
- 2 Respostas
- 2361 Exibições
- Última mensagem por RENATO 7

Ter Mar 22, 2011 14:06
Matemática Financeira
-
- Ajuda- Questão Porcentagem
por DaianedeSousa » Sex Mar 09, 2012 13:24
- 2 Respostas
- 3088 Exibições
- Última mensagem por DaianedeSousa

Sex Mar 09, 2012 21:25
Vestibulares
-
- porcentagem questão complexa
por leandro moraes » Sáb Out 03, 2015 17:25
- 1 Respostas
- 5046 Exibições
- Última mensagem por nakagumahissao

Dom Out 04, 2015 12:17
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 %
%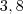 %
%
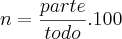
 %
%