 por renanrdaros » Qui Abr 28, 2011 00:29
por renanrdaros » Qui Abr 28, 2011 00:29
![\lim_{x\rightarrow0}\frac{a\sqrt[3]{x+8}-b}{x}=\frac{1}{4} \lim_{x\rightarrow0}\frac{a\sqrt[3]{x+8}-b}{x}=\frac{1}{4}](/latexrender/pictures/471a55837924b1bd87965f937d53ba6a.png)
Determinar o valor das constantes
a e
b
-
renanrdaros
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Mar 19, 2011 19:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. de Computação
- Andamento: cursando
 por LuizAquino » Qui Abr 28, 2011 08:51
por LuizAquino » Qui Abr 28, 2011 08:51
Dica(i) Para que haja uma indeterminação do tipo 0/0, precisamos que
![\lim_{x\to 0} a\sqrt[3]{x+8}-b = 0 \lim_{x\to 0} a\sqrt[3]{x+8}-b = 0](/latexrender/pictures/1c4bb09ae50fe049026af7abdb7de75a.png)
. Disso você deve obter que
b = 2
a.
(ii) Usando (i), você vai precisar resolver a equação
![\lim_{x\to 0}\frac{a\sqrt[3]{x+8}-2a}{x}=\frac{1}{4} \lim_{x\to 0}\frac{a\sqrt[3]{x+8}-2a}{x}=\frac{1}{4}](/latexrender/pictures/f0f6d01bfc6b87f2e176f0f6e7d3c900.png)
.
Note que isso é o mesmo que
![\lim_{x\to 0}\frac{\sqrt[3]{a^3(x+8)}-2a}{x}=\frac{1}{4} \lim_{x\to 0}\frac{\sqrt[3]{a^3(x+8)}-2a}{x}=\frac{1}{4}](/latexrender/pictures/14ef66eb5ed3d0d90de6710baa8c00c6.png)
.
Para resolver o limite no lado esquerdo da equação, multiplique tanto o numerador quanto o denominador por
![\left( \sqrt[3]{[a^3(x+8)]^2}+2a\sqrt[3]{a^3(x+8)} + 4a^2 \right) \left( \sqrt[3]{[a^3(x+8)]^2}+2a\sqrt[3]{a^3(x+8)} + 4a^2 \right)](/latexrender/pictures/4d9bf2bc3515757e005ea03062fa1ed9.png)
. Em seguida, lembre-se do produto notável

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por renanrdaros » Qui Abr 28, 2011 11:02
por renanrdaros » Qui Abr 28, 2011 11:02
LuizAquino escreveu:multiplique tanto o numerador quanto o denominador por
![\left( \sqrt[3]{[a^3(x+8)]^2}+2a\sqrt[3]{a^3(x+8)} + 4a^2 \right) \left( \sqrt[3]{[a^3(x+8)]^2}+2a\sqrt[3]{a^3(x+8)} + 4a^2 \right)](/latexrender/pictures/4d9bf2bc3515757e005ea03062fa1ed9.png)
Luiz, não consegui entender essa parte. Normalmente eu tentaria multiplicar pelo conjugado. Por que você multiplicou por essa expressão?
Obrigado pela ajuda!
EDIT: Depois de enviar a pergunta eu acabei percebendo o porquê da multiplicação por aquela expressão gigante ali.
Editado pela última vez por
renanrdaros em Qui Abr 28, 2011 11:16, em um total de 2 vezes.
-
renanrdaros
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Mar 19, 2011 19:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. de Computação
- Andamento: cursando
 por renanrdaros » Qui Abr 28, 2011 11:08
por renanrdaros » Qui Abr 28, 2011 11:08
Outra coisa que não entendi: Por que você igualou o numerador a zero? Não entendi por que eu preciso que haja uma indeterminação 0/0.
-
renanrdaros
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Mar 19, 2011 19:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. de Computação
- Andamento: cursando
 por renanrdaros » Qui Abr 28, 2011 11:34
por renanrdaros » Qui Abr 28, 2011 11:34
Cheguei no resultado: a=3 e b=6
É isso?
Se for, só falta entender aquela parte da indeterminação do tipo 0/0
-
renanrdaros
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Mar 19, 2011 19:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. de Computação
- Andamento: cursando
 por LuizAquino » Qui Abr 28, 2011 12:16
por LuizAquino » Qui Abr 28, 2011 12:16
Suponha que
![\lim_{x\to 0} a\sqrt[3]{x+8}-b = c \lim_{x\to 0} a\sqrt[3]{x+8}-b = c](/latexrender/pictures/5a257594061199ece2232769a00c5a6b.png)
, com
c uma constante não nula.
Então teríamos o limite:
![\lim_{x\to 0}\frac{a\sqrt[3]{x+8}-b}{x} = \left(\lim_{x\to 0}a\sqrt[3]{x+8}-b\right)\left(\lim_{x\to 0}\frac{1}{x}\right) = c \left(\lim_{x\to 0}\frac{1}{x}\right) \lim_{x\to 0}\frac{a\sqrt[3]{x+8}-b}{x} = \left(\lim_{x\to 0}a\sqrt[3]{x+8}-b\right)\left(\lim_{x\to 0}\frac{1}{x}\right) = c \left(\lim_{x\to 0}\frac{1}{x}\right)](/latexrender/pictures/dbae65bc80361eef4a91923312fe7ccb.png)
Lembre-se que:
(i)
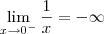
(ii)
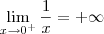
De (i) e (ii) temos que não existe o limite
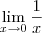
, já que os seus laterais são distintos.
Desse modo, o seu limite original não existiria. Mas, você quer que esse limite exista e seja igual a 1/4. Daí a estratégia de montar a indeterminação do tipo 0/0.
Quanto a saber se sua resposta está certa, você mesmo pode conferir! Basta substituir os valores de
a e
b no limite original e verificar se ele será igual a 1/4.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por renanrdaros » Qui Abr 28, 2011 12:38
por renanrdaros » Qui Abr 28, 2011 12:38
Entendi que eu tenho que manipular a expressão para que o limite exista e seja igual a 1/4, mas não entendi ONDE a indeterminação 0/0 entra nisso.
-
renanrdaros
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Mar 19, 2011 19:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. de Computação
- Andamento: cursando
 por LuizAquino » Qui Abr 28, 2011 14:19
por LuizAquino » Qui Abr 28, 2011 14:19
Em resumo, nós temos uma equação do tipo
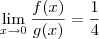
.
Já sabemos no exercício que
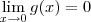
. Além disso, também sabemos que: g(x)<0, se x<0; g(x)>0, se x>0. Isso significa que
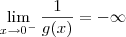
e
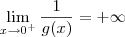
.
Se tivéssemos

, com
c uma constante não nula, então o limite

não existiria e portanto a equação original não seria válida.
Desse modo, precisamos tomar que

.
Ora, mas isso é o mesmo que dizer que o limite original possuirá uma indeterminação do tipo 0/0.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por MarceloFantini » Qui Abr 28, 2011 20:26
por MarceloFantini » Qui Abr 28, 2011 20:26
Normalmente limites de quocientes são finitos (ou seja,

se forem uma indeterminação do tipo

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Por favor, alguém resolve essa questão
por gedeaocosta » Ter Nov 22, 2011 16:12
- 1 Respostas
- 2504 Exibições
- Última mensagem por LuizAquino

Ter Nov 22, 2011 19:32
Logaritmos
-
- Alguém sabe como resolve (5/2)²-5(5/2)+6 passo a passo??
por Elia » Ter Jul 19, 2016 11:28
- 0 Respostas
- 2644 Exibições
- Última mensagem por Elia

Ter Jul 19, 2016 11:28
Sistemas de Equações
-
- Alguém sabe como resolve (5/2)²-5(5/2)+6 passo a passo??
por Elia » Qua Jul 20, 2016 13:57
- 2 Respostas
- 2217 Exibições
- Última mensagem por Elia

Qua Jul 20, 2016 17:51
Equações
-
- [derivada]Alguem pode responder esta questão
por highway » Qua Dez 21, 2011 12:12
- 1 Respostas
- 1675 Exibições
- Última mensagem por LuizAquino

Qua Dez 21, 2011 13:52
Cálculo: Limites, Derivadas e Integrais
-
- Por favor alguém sabe resolver esta questão
por costav13 » Sáb Nov 09, 2013 10:10
- 3 Respostas
- 2578 Exibições
- Última mensagem por e8group

Dom Nov 10, 2013 13:29
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow0}\frac{a\sqrt[3]{x+8}-b}{x}=\frac{1}{4} \lim_{x\rightarrow0}\frac{a\sqrt[3]{x+8}-b}{x}=\frac{1}{4}](/latexrender/pictures/471a55837924b1bd87965f937d53ba6a.png)

![\lim_{x\rightarrow0}\frac{a\sqrt[3]{x+8}-b}{x}=\frac{1}{4} \lim_{x\rightarrow0}\frac{a\sqrt[3]{x+8}-b}{x}=\frac{1}{4}](/latexrender/pictures/471a55837924b1bd87965f937d53ba6a.png)

![\lim_{x\to 0} a\sqrt[3]{x+8}-b = 0 \lim_{x\to 0} a\sqrt[3]{x+8}-b = 0](/latexrender/pictures/1c4bb09ae50fe049026af7abdb7de75a.png) . Disso você deve obter que b = 2a.
. Disso você deve obter que b = 2a.![\lim_{x\to 0}\frac{a\sqrt[3]{x+8}-2a}{x}=\frac{1}{4} \lim_{x\to 0}\frac{a\sqrt[3]{x+8}-2a}{x}=\frac{1}{4}](/latexrender/pictures/f0f6d01bfc6b87f2e176f0f6e7d3c900.png) .
.![\lim_{x\to 0}\frac{\sqrt[3]{a^3(x+8)}-2a}{x}=\frac{1}{4} \lim_{x\to 0}\frac{\sqrt[3]{a^3(x+8)}-2a}{x}=\frac{1}{4}](/latexrender/pictures/14ef66eb5ed3d0d90de6710baa8c00c6.png) .
.![\left( \sqrt[3]{[a^3(x+8)]^2}+2a\sqrt[3]{a^3(x+8)} + 4a^2 \right) \left( \sqrt[3]{[a^3(x+8)]^2}+2a\sqrt[3]{a^3(x+8)} + 4a^2 \right)](/latexrender/pictures/4d9bf2bc3515757e005ea03062fa1ed9.png) . Em seguida, lembre-se do produto notável
. Em seguida, lembre-se do produto notável  .
.



![\lim_{x\to 0} a\sqrt[3]{x+8}-b = c \lim_{x\to 0} a\sqrt[3]{x+8}-b = c](/latexrender/pictures/5a257594061199ece2232769a00c5a6b.png) , com c uma constante não nula.
, com c uma constante não nula.![\lim_{x\to 0}\frac{a\sqrt[3]{x+8}-b}{x} = \left(\lim_{x\to 0}a\sqrt[3]{x+8}-b\right)\left(\lim_{x\to 0}\frac{1}{x}\right) = c \left(\lim_{x\to 0}\frac{1}{x}\right) \lim_{x\to 0}\frac{a\sqrt[3]{x+8}-b}{x} = \left(\lim_{x\to 0}a\sqrt[3]{x+8}-b\right)\left(\lim_{x\to 0}\frac{1}{x}\right) = c \left(\lim_{x\to 0}\frac{1}{x}\right)](/latexrender/pictures/dbae65bc80361eef4a91923312fe7ccb.png)
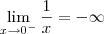
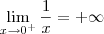
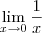 , já que os seus laterais são distintos.
, já que os seus laterais são distintos.

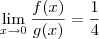 .
.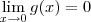 . Além disso, também sabemos que: g(x)<0, se x<0; g(x)>0, se x>0. Isso significa que
. Além disso, também sabemos que: g(x)<0, se x<0; g(x)>0, se x>0. Isso significa que 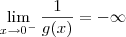 e
e 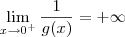 .
. , com c uma constante não nula, então o limite
, com c uma constante não nula, então o limite  não existiria e portanto a equação original não seria válida.
não existiria e portanto a equação original não seria válida. .
.
 se forem uma indeterminação do tipo
se forem uma indeterminação do tipo  .
.

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.