O que você escreveu (concertando a letra "A"), foi:
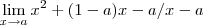
Colocando isso em uma notação mais conveniente, o que você de fato escreveu foi:

Mas, ao que parece, o que você quer é:
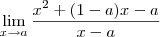
Considerando que seja esse o limite que você desejava, para ter escrito isso na notação que você usou, então você deveria ter escrito algo como:
![\lim_{x\rightarrow a}[x^2+(1-a)x-a]/(x-a) \lim_{x\rightarrow a}[x^2+(1-a)x-a]/(x-a)](/latexrender/pictures/62d2eed49fe1f968cabdbe707f649751.png)
Seja mais cuidadoso com o uso dos delimitadores adequados, isto é, com o uso dos símbolos "()", "[]" e "{}".
Agora, vamos ao exercício.
O que você precisa é fatorar o numerador. Note que
a é raiz do polinômio
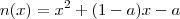
. Isso significa que

, onde x' é a outra raiz de n(x).
O seu trabalho então será determinar essa outra raiz. Existem várias formas de fazer isso. Mas, o mais simples nesse caso talvez seja você perceber que a soma das raízes deve ser igual a -(1 -
a)/2.
ObservaçãoO erro da letra "A" que apareceu deve-se ao fato de você ter escrito "x²" ou invés de "x^2" dentro do ambiente tex.




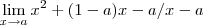

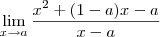
![\lim_{x\rightarrow a}[x^2+(1-a)x-a]/(x-a) \lim_{x\rightarrow a}[x^2+(1-a)x-a]/(x-a)](/latexrender/pictures/62d2eed49fe1f968cabdbe707f649751.png)
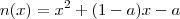 . Isso significa que
. Isso significa que  , onde x' é a outra raiz de n(x).
, onde x' é a outra raiz de n(x).