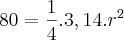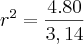por Alexander » Sáb Abr 23, 2011 12:08
por Alexander » Sáb Abr 23, 2011 12:08
Olá!
Uns dias atrás estava tentando resolver essa questão de fundamental:
(EAM) Um cavalo deve ser amarrado a uma estaca situada em um dos vértices de um pasto que tem a forma de um quadrado, cujo lado mede 20m. Para que ele possa pastar em cerca de 20% da área total do pasto, a parte inteira, em metros, do comprimento da corda que o prende à estaca deve ser igual a:
A: 1 B:2 C:5 D:8 E:10
Eu estou absolutamente embolado nessa questão.
Um colega meu me explicou pela lógica, sem cálculo, e mesmo assim eu não entendi.
Eu tentei aqui agora calculando a diagonal dele. Um quadrado, lado 20, 20%=4. d=l.
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
=> d=4.
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
=> 4.1,41=5,64.
Só que, a resposta certa é 10.
Eu fui até onde eu consegui.
Ajudem!
Aloha!
"Se não puder se destacar pelo talento, vença pelo esforço." - Dave Weinbaum
-
Alexander
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Nov 24, 2010 23:10
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por SidneySantos » Sáb Abr 23, 2011 12:51
por SidneySantos » Sáb Abr 23, 2011 12:51
Área Total do pasto: 20² = 400 m²
Área em que o cavalo pode pastar: 0,2.400 = 80 m²
Comprimento da Corda:
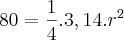
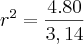 r = 10,09 mLetra E
r = 10,09 mLetra E
Um forte abraço e bom estudo!!!
-
SidneySantos
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Qua Abr 20, 2011 07:47
- Localização: Belém - Pará
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Educaçao Matemática
- Andamento: cursando
 por Alexander » Dom Abr 24, 2011 11:15
por Alexander » Dom Abr 24, 2011 11:15
Wow! Obrigada!
Abraços.
"Se não puder se destacar pelo talento, vença pelo esforço." - Dave Weinbaum
-
Alexander
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Nov 24, 2010 23:10
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Porcentagem, area do quadrado
por lucas7 » Ter Mar 01, 2011 09:51
- 3 Respostas
- 7836 Exibições
- Última mensagem por lucas7

Ter Mar 01, 2011 13:47
Problemas do Cotidiano
-
- Área do quadrado
por Andreza » Ter Jan 03, 2012 10:43
- 2 Respostas
- 1992 Exibições
- Última mensagem por fraol

Ter Jan 03, 2012 13:54
Geometria Plana
-
- Área do Quadrado
por Pri Ferreira » Qua Mar 21, 2012 14:35
- 3 Respostas
- 2302 Exibições
- Última mensagem por ednaldo1982

Sáb Mar 31, 2012 11:48
Geometria Plana
-
- Mostre que a área do quadrado é menor que a do hexagono
por andersontricordiano » Qua Abr 06, 2011 16:30
- 1 Respostas
- 2024 Exibições
- Última mensagem por Elcioschin

Qua Abr 06, 2011 18:04
Geometria Plana
-
- Calcular perímetro do quadrado] através da área do triângulo
 por lukasmetal » Qua Nov 30, 2011 12:11
por lukasmetal » Qua Nov 30, 2011 12:11
- 3 Respostas
- 3851 Exibições
- Última mensagem por lukasmetal

Qui Dez 01, 2011 12:19
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) => d=4.
=> d=4.![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) => 4.1,41=5,64.
=> 4.1,41=5,64.