 por gabrielsdg » Qua Abr 20, 2011 16:41
por gabrielsdg » Qua Abr 20, 2011 16:41
Olá galera,
Tô apanhando em limites, o professor passou uma lista de exercícios e eu não entendi nada do assunto!
Quem me ajudar dou um bju na boca!

(brincadeira!)
Vai lá a primeira questão
1) Calcule os seguintes LIMITES:
a)
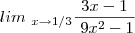
b)

c)
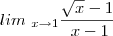
-
gabrielsdg
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Abr 20, 2011 16:27
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por LuizAquino » Qua Abr 20, 2011 17:23
por LuizAquino » Qua Abr 20, 2011 17:23
O trabalho maior no cálculo dos limites é a fatoração e a simplificação que precisamos fazer para remover indeterminações. Por isso, eu recomendo que revise esses conteúdos.
Por exemplo, veja a solução do primeiro exercício.
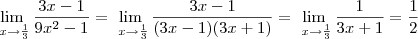
.
Agora, tente fazer os outros exercícios.
SugestõesEu acredito que os tópicos abaixo vão lhe interessar.
Aulas de Matemática no YouTubeviewtopic.php?f=120&t=3818Curso de Cálculo I no YouTubeviewtopic.php?f=137&t=4280
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculando a derivada
por Ana Maria da Silva » Sáb Set 07, 2013 11:47
- 1 Respostas
- 1406 Exibições
- Última mensagem por Man Utd

Dom Set 15, 2013 01:05
Cálculo: Limites, Derivadas e Integrais
-
- Calculando F(x) derivada
por Ana Maria da Silva » Ter Set 10, 2013 09:52
- 2 Respostas
- 1923 Exibições
- Última mensagem por Ana Maria da Silva

Qua Set 11, 2013 19:09
Cálculo: Limites, Derivadas e Integrais
-
- calculando dy/dx obtemos?
por Ana Maria da Silva » Qua Set 11, 2013 21:50
- 0 Respostas
- 842 Exibições
- Última mensagem por Ana Maria da Silva

Qua Set 11, 2013 21:50
Cálculo: Limites, Derivadas e Integrais
-
- [Matriz]- Calculando a inversa
por Ana_Rodrigues » Seg Mar 26, 2012 19:05
- 1 Respostas
- 1167 Exibições
- Última mensagem por fraol

Seg Mar 26, 2012 21:44
Matrizes e Determinantes
-
- Calculando a area de um triangulo
por bencz » Qui Jul 05, 2012 16:15
- 1 Respostas
- 1207 Exibições
- Última mensagem por MarceloFantini

Qui Jul 05, 2012 18:49
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
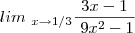

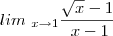

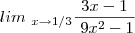

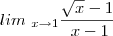

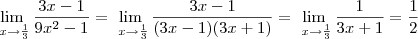 .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)