 por jamiel » Sex Abr 15, 2011 13:59
por jamiel » Sex Abr 15, 2011 13:59
Se alguém puder dar uma ajudinha eu agradeço!
x-2 / x+3 ? x / x+2
1º passo
(x+2)(x-2) -(x+3)x / (x+3)(x+2) ? 0
2º passo
(x²+2x-2x-4) -(x²-3x) ? 0
Minha dúvida é justamente nesse segundo passo, pois eu consigo "3x-4". No gabarito, "3x+4", não entendo onde posso ter errado. No caso 3x-4, x seria = 4/3, mas no do gabarito x = -4/3. Alguém pode me ajudar?
A formatação de formulas tá dando bronca pra mim, tive q fazer assim mesmo!
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por MarceloFantini » Sex Abr 15, 2011 16:30
por MarceloFantini » Sex Abr 15, 2011 16:30
Partindo do primeiro passo:
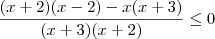

Detalhando:
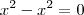
, sobra

no numerador. Coloquei

em evidência, e depois multipliquei tudo e inverti a desigualdade.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jamiel » Sex Abr 15, 2011 16:39
por jamiel » Sex Abr 15, 2011 16:39
Fantini ---- thank you a lot!
Ok! Então, quer dizer que se -3x -4 ? 0 q é o numerador ---> 3x + 4 ? 0 ... inverte-se o donominador também, melhor dizendo, os denominadores agregados? Pq disso?
Mais uma vez, thank for your help!
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por MarceloFantini » Sex Abr 15, 2011 17:08
por MarceloFantini » Sex Abr 15, 2011 17:08
Não inverti o denominador, note que ele ficou inalterado.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jamiel » Sex Abr 15, 2011 22:38
por jamiel » Sex Abr 15, 2011 22:38
Thank you one more!
Deixa-me ver se entendi:
O denominador permance inalterado devido às operações já feitas anteriormente com o numerador?
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por MarceloFantini » Sex Abr 15, 2011 22:41
por MarceloFantini » Sex Abr 15, 2011 22:41
Neste caso, sim.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jamiel » Sáb Abr 23, 2011 00:18
por jamiel » Sáb Abr 23, 2011 00:18
Sabe-se que a parábola que representa a função y = -x²+bx+c passa pelo ponto (3;5) e que seu vértice é (m;5/4). Calcule b,c e m.
-b/2•(-1) = m (1)
-?/4•(-1) = 5/4 ---- 5/4•-4 = -20/4 = -5² = ?25 = 5 --->
-[b² -4•(-1)•c] / 4•(-1) = 5/4
b² -4c("?25 =5") = 5 (2)
-(3)² + 3b + c = -5
-9 + 3b + c = -5
3b + c = 4 (3)
Sistema ---->
b² + 4c = 5
3b + c = 4
Aqui é q eu não consegui ir adiante. Se eu considerar o "c=4", obtenho o valor de b²=-11 ---- -11/-2 = "m = 11/2". Porém, não senti precisão, mais, teria q obter mais um "c=-29", o q seria meio contraditório. A coordenadas são (11;-29) e (1;1), no gabarito!
Alguém pode me ajudar nessa? Agrandeço desde já!
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por MarceloFantini » Sáb Abr 23, 2011 13:16
por MarceloFantini » Sáb Abr 23, 2011 13:16
Jamiel, por favor crie um novo tópico para sua dúvida, isso contribui para a organização do fórum.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jamiel » Sáb Abr 23, 2011 13:26
por jamiel » Sáb Abr 23, 2011 13:26
Vlw pelo toque ... irei criar outro!
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida na resolução
por Du21 » Sex Mar 04, 2011 20:48
- 2 Respostas
- 1748 Exibições
- Última mensagem por Du21

Sáb Mar 05, 2011 00:07
Sistemas de Equações
-
- Dúvida - resolução
por marinalcd » Ter Out 15, 2013 20:00
- 0 Respostas
- 955 Exibições
- Última mensagem por marinalcd

Ter Out 15, 2013 20:00
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida na Resolução de uma Função
 por brunnomaia » Dom Mar 06, 2011 11:07
por brunnomaia » Dom Mar 06, 2011 11:07
- 2 Respostas
- 1808 Exibições
- Última mensagem por brunnomaia

Dom Mar 06, 2011 11:53
Funções
-
- Dúvida - resolução função !
 por jamiel » Qui Mai 26, 2011 18:07
por jamiel » Qui Mai 26, 2011 18:07
- 11 Respostas
- 5916 Exibições
- Última mensagem por jamiel

Qui Mai 26, 2011 22:31
Funções
-
- Função Sen - Dúvida Resolução
por jamiel » Sáb Jul 02, 2011 17:47
- 7 Respostas
- 4475 Exibições
- Última mensagem por jamiel

Sáb Jul 02, 2011 19:42
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


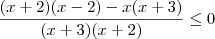

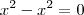 , sobra
, sobra  no numerador. Coloquei
no numerador. Coloquei  em evidência, e depois multipliquei tudo e inverti a desigualdade.
em evidência, e depois multipliquei tudo e inverti a desigualdade.



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.