Boa tarde
Bom, eu penso que o que você deverá ter é uma função definida por ramos do género

se x<0,
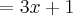
se

e,
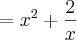
se x>2
Se voce quer saber se é contínua nos pontos x=0 e x=2 terá que calcular o limite da função nesses pontos, ou seja,

e
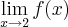
. Isto vai lhe dar a continuidade da função nestes dois pontos. Mas se voce quiser saber a continuidade lateral, já vai ter que calcular para cada ponto o limite à direita e à esquerda do ponto.
Por exemplo plara x=0 faz

e

. e o resultado vai lhe permitir dizer se a função é continua à direita, à esquerda, ou à direita e à esquerda do ponto que está a estudar.
Para calcular o limite basta substituir o x na função pelo valor do ponto que está a estudar. Para o ponto x=0 substitui o x da função por 0, e para o 2 a mesma coisa.
Quanto aos zeros, para saber o
c e o
K já vai utilizar o Teorema de Bolzano.
Para saber se existe um
c tem que ter um intervalo onde a função seja contínua, e calcular a imagem dos valores desse intervalo.
Por exemplo se o intervalo for (2,5), calcula a imagem de 2 e a imagem de 5, depois vê se o valor de
k dado está entre essas imagens que vce calculou. se estiver é porque existe pelo menos um
c.
Para o Zero utiliza-se o corolário do Teorema de Bolzano.
Calculam-se as imagens dos pontos do intervalo dado, e multiplicam-se uma pela outra. para que exista pelo menos um zero, o resultado dessa multiplicação tem que ser inferior a zero: f(a)*f(b)<0, se isto ocorrer, há pelo menos um zero.
Espero ter ajudado!
Boa sorte
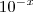 se x<0
se x<0 para x=0 e para x=2
para x=0 e para x=2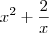 se x>2
se x>2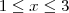


 se x<0,
se x<0, 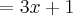 se
se  e,
e, 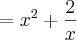 se x>2
se x>2 e
e 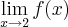 . Isto vai lhe dar a continuidade da função nestes dois pontos. Mas se voce quiser saber a continuidade lateral, já vai ter que calcular para cada ponto o limite à direita e à esquerda do ponto.
. Isto vai lhe dar a continuidade da função nestes dois pontos. Mas se voce quiser saber a continuidade lateral, já vai ter que calcular para cada ponto o limite à direita e à esquerda do ponto. e
e  . e o resultado vai lhe permitir dizer se a função é continua à direita, à esquerda, ou à direita e à esquerda do ponto que está a estudar.
. e o resultado vai lhe permitir dizer se a função é continua à direita, à esquerda, ou à direita e à esquerda do ponto que está a estudar.

