 por Abelardo » Sáb Abr 09, 2011 19:11
por Abelardo » Sáb Abr 09, 2011 19:11
Considere uma função

não-constante e tal que
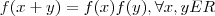
. Das afirmações :
I)
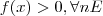
naturais não-nulos
II)
![f(nx)= {[f(x)]}^{n}, \forall x E f(nx)= {[f(x)]}^{n}, \forall x E](/latexrender/pictures/c08b8d884ee44470260ef2f39dcd656a.png)
Reais,

naturais não-nulos
III)
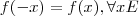
Reais.
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Sáb Abr 09, 2011 19:45
por Molina » Sáb Abr 09, 2011 19:45
Aberlado, o que pretende-se nesta questão?
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Abelardo » Sáb Abr 09, 2011 21:21
por Abelardo » Sáb Abr 09, 2011 21:21
Desculpe-me Molina, esqueci o resto...
Completando a questão ''é (são) verdadeiras?'' A questão quer saber qual delas é verdadeira, mas eu fiquei flutuando porque diz que a função é não-constante!! Se puderes fazer um comentário sobre isso, ficaria muito grato.
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Dom Abr 10, 2011 00:08
por Molina » Dom Abr 10, 2011 00:08
Boa noite, Abelardo.
Acho que neste contexto o termo
não constante refere-se a função ser diferente de

. Ou seja, a função terá valor a independente do x escolhido. Exemplos:
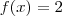


etc.
Voltando a sua questão, no item I) você cita

, porém não há
n na função. [Esclareça se não há algum erro de digitação]

No item II) temos que:
![f(nx)=f(x + x + ... + x)=f(x)*f(x)*...*f(x)=[f(x)]^n \Rightarrow f(nx)=[f(x)]^n f(nx)=f(x + x + ... + x)=f(x)*f(x)*...*f(x)=[f(x)]^n \Rightarrow f(nx)=[f(x)]^n](/latexrender/pictures/d657a1c42edeb21a914f66fffaaec564.png)

Não estou conseguindo provar o item III)
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Abelardo » Dom Abr 10, 2011 00:15
por Abelardo » Dom Abr 10, 2011 00:15
há sim erro de digitação, como sofro sem saber colocar o símbolo dos número naturais e dos reais..
Na primeira afirmação tem sim um erro, qualquer que seja ''X'' pertencente aos números reais.
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por VtinxD » Dom Abr 10, 2011 02:30
por VtinxD » Dom Abr 10, 2011 02:30
Essa equação funcional tem solução igual a
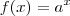
,mas não é necessário saber disso para resolver a questão.Ja vou assumir a prova do molina do segundo e provar que o terceiro é falso, para poder provar o primeiro.
3°
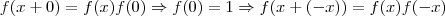

Perceba que f(x) não pode ser igual a zero pois se não f(-x) não estaria definido ,contradizendo assim o fato de que f(x) está definido para todo x.
1°

.Como
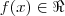
então

e como f(x) é diferente de 0 ,temos:

e como isto é valido para todo x real então se x=y/2 tambem vai ser valido para todo y real,logo

.
Espero ter ajudado
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Probabilidade-introdução
por Jeenae » Dom Abr 05, 2009 00:47
- 1 Respostas
- 4870 Exibições
- Última mensagem por lucasguedes

Qui Jun 25, 2009 19:53
Estatística
-
- [Cálculo] Introdução
por Gabriel_DvT » Sex Mar 30, 2012 11:22
- 1 Respostas
- 1439 Exibições
- Última mensagem por LuizAquino

Sex Mar 30, 2012 17:48
Cálculo: Limites, Derivadas e Integrais
-
- provas de Introdução à Análise
por ferbonin » Dom Ago 05, 2007 23:08
- 1 Respostas
- 2789 Exibições
- Última mensagem por admin

Ter Ago 28, 2007 03:08
Pedidos de Materiais
-
- Introdução Álgebra Linear
por Cicero ferreira » Sex Mar 14, 2014 18:02
- 0 Respostas
- 966 Exibições
- Última mensagem por Cicero ferreira

Sex Mar 14, 2014 18:02
Álgebra I para Licenciatura
-
- Introdução ao cálculo - [Simplificação]
por EDGLE1984 » Seg Ago 18, 2014 13:31
- 1 Respostas
- 1063 Exibições
- Última mensagem por DanielFerreira

Sáb Ago 23, 2014 22:41
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 não-constante e tal que
não-constante e tal que 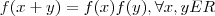 . Das afirmações :
. Das afirmações :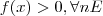 naturais não-nulos
naturais não-nulos![f(nx)= {[f(x)]}^{n}, \forall x E f(nx)= {[f(x)]}^{n}, \forall x E](/latexrender/pictures/c08b8d884ee44470260ef2f39dcd656a.png) Reais,
Reais,  naturais não-nulos
naturais não-nulos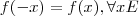 Reais.
Reais.
 não-constante e tal que
não-constante e tal que 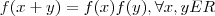 . Das afirmações :
. Das afirmações :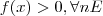 naturais não-nulos
naturais não-nulos![f(nx)= {[f(x)]}^{n}, \forall x E f(nx)= {[f(x)]}^{n}, \forall x E](/latexrender/pictures/c08b8d884ee44470260ef2f39dcd656a.png) Reais,
Reais,  naturais não-nulos
naturais não-nulos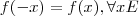 Reais.
Reais.


 . Ou seja, a função terá valor a independente do x escolhido. Exemplos:
. Ou seja, a função terá valor a independente do x escolhido. Exemplos: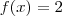


 , porém não há n na função. [Esclareça se não há algum erro de digitação]
, porém não há n na função. [Esclareça se não há algum erro de digitação] 
![f(nx)=f(x + x + ... + x)=f(x)*f(x)*...*f(x)=[f(x)]^n \Rightarrow f(nx)=[f(x)]^n f(nx)=f(x + x + ... + x)=f(x)*f(x)*...*f(x)=[f(x)]^n \Rightarrow f(nx)=[f(x)]^n](/latexrender/pictures/d657a1c42edeb21a914f66fffaaec564.png)



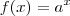 ,mas não é necessário saber disso para resolver a questão.Ja vou assumir a prova do molina do segundo e provar que o terceiro é falso, para poder provar o primeiro.
,mas não é necessário saber disso para resolver a questão.Ja vou assumir a prova do molina do segundo e provar que o terceiro é falso, para poder provar o primeiro.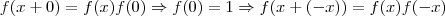

 .Como
.Como 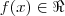 então
então  e como f(x) é diferente de 0 ,temos:
e como f(x) é diferente de 0 ,temos: e como isto é valido para todo x real então se x=y/2 tambem vai ser valido para todo y real,logo
e como isto é valido para todo x real então se x=y/2 tambem vai ser valido para todo y real,logo  .
.