Fundamentos da Matemática Elementar -Gelson Iezzi e Murakami

[Abelardo]

Estou postando dessas forma, porque não tenho o livro mas copiei as duas perguntas. Achei que copiando as perguntas facilitaria para os que tem o livro ou tem acesso a ele. Vamos lá


Página 105 do volume 1 (8ª edição) questão número 178. ''De uma caixa contendo bolas brancas e pretas, retiraram-se 15 brancas, ficando a relação de 1 branca para 2 pretas. Em seguida, retiraram-se 10 pretas, restando, na caixa, bolas na razão de 4 brancas para 3 pretas. Determine quantas bolas havia, inicialmente, na caixa.''

Página 110 do volume 1 (8ª edição) questão número 192. (Como consegui a imagem na net). ''Qual o menor número inteiro de voltas que deve dar a roda c da engrenagem da figura, para que a roda a dê um número interios de voltas?''


A segunda questão nem faço ideia de como começar, ele não dá nenhuma relação entre as engrenagens, nada mesmo, nem o raio de uma figura.. ai travei na hora kkk.

[Fabricio dalla]

a primeira questao qual é a resposta ?39?
a segunda questão se faz por MMC

[Abelardo]

O número de bolas é 39 mesmo, mas como foi que você fez?

Como aplicar MMC na questão das engrenagens? Quais valores? Admitindo incógnitas?

[Fabricio dalla]

caixa de bolas=Cb
B=bolas brancas
P=bolas pretas

Cb=B+P
em que, para primeira retirada sendo elas bolas brancas temos B=x-15 e P=y
logo tem-se Cb=x-15+P,Cb=x-15+y

onde:
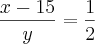
y=2x-30
em que para segunda retirada sendo elas de bolas pretas temos B=x-15 e P=y-10
Cb=x-15+y-10
onde:
3x-45=4y-40
3x-45=4(2x-30)-40
5x=115,x=23
y=2(23)-30
y=16,onde 16+23=39

[Abelardo]

Super legal essa resolução. Mas como se faz a das engrenagens?