Olá, bom dia!
Estou com uma dúvida que pode parecer boba para quem está afiado em matemática! Mas para quem está voltando agora a rever conceitos antigos, é uma complicação! Voltei a estudar para concursos, e empanquei em uma questão por um motivo bobo... Dúvida em como calcular a potência... Alguém poderia me ajudar?
A dúvida é a seguinte: 8^2/3 quanto dá? Como faço mesmo para resolver?
O erro é parar de estudar, quando se volta está enferrujado até nos pequenos detalhes ...
Obrigada
.
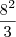. Uma outra forma correta de escrever essa expressão seria 8^(2/3).![a^\frac{p}{q} = \sqrt[q]{a^p} = \left(\sqrt[q]{a}\right)^p](/latexrender/pictures/7833f2c7b5abeb6dd4121fe4e920a097.png "a^\frac{p}{q} = \sqrt[q]{a^p} = \left(\sqrt[q]{a}\right)^p")
.![8^\frac{2}{3} = \sqrt[3]{8^2} = \left(\sqrt[3]{8}\right)^2 = 2^2 = 4](/latexrender/pictures/5f67b4c3feb44e30fd9a2de45d53a8e5.png "8^\frac{2}{3} = \sqrt[3]{8^2} = \left(\sqrt[3]{8}\right)^2 = 2^2 = 4")
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)