 por guillcn » Qui Abr 07, 2011 20:40
por guillcn » Qui Abr 07, 2011 20:40
O exercicio e o seguinnte :
O valor de real A,para que se tenha
![A . \sqrt[2]{3} = {\left(2 + \sqrt[2]{3} \right)}^{3}-{\left(2 - \sqrt[2]{3} \right)}^{3} A . \sqrt[2]{3} = {\left(2 + \sqrt[2]{3} \right)}^{3}-{\left(2 - \sqrt[2]{3} \right)}^{3}](/latexrender/pictures/72388fd9be74a5d2281a2f5b3852a9c9.png)
entao passei raiz para o outro lado
![A = \frac{{\left(2 + \sqrt[2]{3} \right)}^{3}-{\left(2 - \sqrt[2]{3} \right)}^{3}}{\sqrt[2]{3}} A = \frac{{\left(2 + \sqrt[2]{3} \right)}^{3}-{\left(2 - \sqrt[2]{3} \right)}^{3}}{\sqrt[2]{3}}](/latexrender/pictures/c84b1397d96248a77ae27b62580f5353.png)
porem quando se tira o cubo perfeito das partes sempre resta uma raiz de tres
![\frac{\left(8+12\sqrt[2]{3}+18 + 9 \right)\left(8 - 12\sqrt[2]{3}+ 18 - 9\right)}{\sqrt[2]{3}} \frac{\left(8+12\sqrt[2]{3}+18 + 9 \right)\left(8 - 12\sqrt[2]{3}+ 18 - 9\right)}{\sqrt[2]{3}}](/latexrender/pictures/4dc2551835be4220388c45b56b2fd9f9.png)
=
![\frac{\left(35 + 12\sqrt[2]{3}\right)-\left(17 - 12\sqrt[2]{3}\right) }{\sqrt[2]{3}} \frac{\left(35 + 12\sqrt[2]{3}\right)-\left(17 - 12\sqrt[2]{3}\right) }{\sqrt[2]{3}}](/latexrender/pictures/f02a543df354c80b3b4cd5734bf8654b.png)
como posso resolver esse problema obrigado pela atençao.
-
guillcn
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Ter Abr 05, 2011 16:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por FilipeCaceres » Qui Abr 07, 2011 21:04
por FilipeCaceres » Qui Abr 07, 2011 21:04
Observe que:
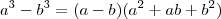
Agora chame,
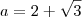
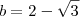
Substituindo os valores você encontrará

Espero que ajude, se persistir com dúvida é so perguntar.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por guillcn » Qui Abr 07, 2011 21:09
por guillcn » Qui Abr 07, 2011 21:09
ok.obrigado pela ajuda.
-
guillcn
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Ter Abr 05, 2011 16:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por FilipeCaceres » Qui Abr 07, 2011 21:16
por FilipeCaceres » Qui Abr 07, 2011 21:16
Da forma que você fez também deveria ter encontrado o mesmo valor, o problema foi que
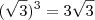
e não
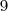
como você colocou, se você corrigir este errinho encontrará a resposta.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- cubo perfeito
por guillcn » Qui Abr 07, 2011 20:42
- 2 Respostas
- 1234 Exibições
- Última mensagem por guillcn

Qui Abr 07, 2011 21:13
Álgebra Elementar
-
- Quadrado Perfeito?
por Molina » Qui Nov 25, 2010 17:00
- 6 Respostas
- 6688 Exibições
- Última mensagem por pedroaugustox47

Sex Mai 11, 2012 16:28
Desafios Difíceis
-
- Quadrado perfeito
por guillcn » Ter Abr 05, 2011 19:15
- 2 Respostas
- 2522 Exibições
- Última mensagem por guillcn

Ter Abr 05, 2011 19:54
Álgebra Elementar
-
- Ajuda com quadrado perfeito
por joaoalbertotb » Ter Ago 25, 2009 13:01
- 2 Respostas
- 2314 Exibições
- Última mensagem por joaoalbertotb

Qua Ago 26, 2009 12:20
Trigonometria
-
- Trinômio Quadrado Perfeito
por Balanar » Ter Ago 10, 2010 22:48
- 2 Respostas
- 4924 Exibições
- Última mensagem por DanielFerreira

Dom Jan 08, 2012 18:05
Desafios Difíceis
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![A . \sqrt[2]{3} = {\left(2 + \sqrt[2]{3} \right)}^{3}-{\left(2 - \sqrt[2]{3} \right)}^{3} A . \sqrt[2]{3} = {\left(2 + \sqrt[2]{3} \right)}^{3}-{\left(2 - \sqrt[2]{3} \right)}^{3}](/latexrender/pictures/72388fd9be74a5d2281a2f5b3852a9c9.png)
![A = \frac{{\left(2 + \sqrt[2]{3} \right)}^{3}-{\left(2 - \sqrt[2]{3} \right)}^{3}}{\sqrt[2]{3}} A = \frac{{\left(2 + \sqrt[2]{3} \right)}^{3}-{\left(2 - \sqrt[2]{3} \right)}^{3}}{\sqrt[2]{3}}](/latexrender/pictures/c84b1397d96248a77ae27b62580f5353.png)
![\frac{\left(8+12\sqrt[2]{3}+18 + 9 \right)\left(8 - 12\sqrt[2]{3}+ 18 - 9\right)}{\sqrt[2]{3}} \frac{\left(8+12\sqrt[2]{3}+18 + 9 \right)\left(8 - 12\sqrt[2]{3}+ 18 - 9\right)}{\sqrt[2]{3}}](/latexrender/pictures/4dc2551835be4220388c45b56b2fd9f9.png) =
= ![\frac{\left(35 + 12\sqrt[2]{3}\right)-\left(17 - 12\sqrt[2]{3}\right) }{\sqrt[2]{3}} \frac{\left(35 + 12\sqrt[2]{3}\right)-\left(17 - 12\sqrt[2]{3}\right) }{\sqrt[2]{3}}](/latexrender/pictures/f02a543df354c80b3b4cd5734bf8654b.png)

![A . \sqrt[2]{3} = {\left(2 + \sqrt[2]{3} \right)}^{3}-{\left(2 - \sqrt[2]{3} \right)}^{3} A . \sqrt[2]{3} = {\left(2 + \sqrt[2]{3} \right)}^{3}-{\left(2 - \sqrt[2]{3} \right)}^{3}](/latexrender/pictures/72388fd9be74a5d2281a2f5b3852a9c9.png)
![A = \frac{{\left(2 + \sqrt[2]{3} \right)}^{3}-{\left(2 - \sqrt[2]{3} \right)}^{3}}{\sqrt[2]{3}} A = \frac{{\left(2 + \sqrt[2]{3} \right)}^{3}-{\left(2 - \sqrt[2]{3} \right)}^{3}}{\sqrt[2]{3}}](/latexrender/pictures/c84b1397d96248a77ae27b62580f5353.png)
![\frac{\left(8+12\sqrt[2]{3}+18 + 9 \right)\left(8 - 12\sqrt[2]{3}+ 18 - 9\right)}{\sqrt[2]{3}} \frac{\left(8+12\sqrt[2]{3}+18 + 9 \right)\left(8 - 12\sqrt[2]{3}+ 18 - 9\right)}{\sqrt[2]{3}}](/latexrender/pictures/4dc2551835be4220388c45b56b2fd9f9.png) =
= ![\frac{\left(35 + 12\sqrt[2]{3}\right)-\left(17 - 12\sqrt[2]{3}\right) }{\sqrt[2]{3}} \frac{\left(35 + 12\sqrt[2]{3}\right)-\left(17 - 12\sqrt[2]{3}\right) }{\sqrt[2]{3}}](/latexrender/pictures/f02a543df354c80b3b4cd5734bf8654b.png)

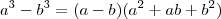
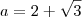
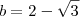



 e não
e não 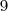 como você colocou, se você corrigir este errinho encontrará a resposta.
como você colocou, se você corrigir este errinho encontrará a resposta.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.