O valor de real A,para que se tenha
![A . \sqrt[2]{3} = {\left(2 + \sqrt[2]{3} \right)}^{3}-{\left(2 - \sqrt[2]{3} \right)}^{3} A . \sqrt[2]{3} = {\left(2 + \sqrt[2]{3} \right)}^{3}-{\left(2 - \sqrt[2]{3} \right)}^{3}](/latexrender/pictures/72388fd9be74a5d2281a2f5b3852a9c9.png)
entao passei raiz para o outro lado
![A = \frac{{\left(2 + \sqrt[2]{3} \right)}^{3}-{\left(2 - \sqrt[2]{3} \right)}^{3}}{\sqrt[2]{3}} A = \frac{{\left(2 + \sqrt[2]{3} \right)}^{3}-{\left(2 - \sqrt[2]{3} \right)}^{3}}{\sqrt[2]{3}}](/latexrender/pictures/c84b1397d96248a77ae27b62580f5353.png)
porem quando se tira o cubo perfeito das partes sempre resta uma raiz de tres
![\frac{\left(8+12\sqrt[2]{3}+18 + 9 \right)\left(8 - 12\sqrt[2]{3}+ 18 - 9\right)}{\sqrt[2]{3}} \frac{\left(8+12\sqrt[2]{3}+18 + 9 \right)\left(8 - 12\sqrt[2]{3}+ 18 - 9\right)}{\sqrt[2]{3}}](/latexrender/pictures/4dc2551835be4220388c45b56b2fd9f9.png) =
= ![\frac{\left(35 + 12\sqrt[2]{3}\right)-\left(17 - 12\sqrt[2]{3}\right) }{\sqrt[2]{3}} \frac{\left(35 + 12\sqrt[2]{3}\right)-\left(17 - 12\sqrt[2]{3}\right) }{\sqrt[2]{3}}](/latexrender/pictures/f02a543df354c80b3b4cd5734bf8654b.png)
como posso resolver esse problema obrigado pela atençao.

![A . \sqrt[2]{3} = {\left(2 + \sqrt[2]{3} \right)}^{3}-{\left(2 - \sqrt[2]{3} \right)}^{3} A . \sqrt[2]{3} = {\left(2 + \sqrt[2]{3} \right)}^{3}-{\left(2 - \sqrt[2]{3} \right)}^{3}](/latexrender/pictures/72388fd9be74a5d2281a2f5b3852a9c9.png)
![A = \frac{{\left(2 + \sqrt[2]{3} \right)}^{3}-{\left(2 - \sqrt[2]{3} \right)}^{3}}{\sqrt[2]{3}} A = \frac{{\left(2 + \sqrt[2]{3} \right)}^{3}-{\left(2 - \sqrt[2]{3} \right)}^{3}}{\sqrt[2]{3}}](/latexrender/pictures/c84b1397d96248a77ae27b62580f5353.png)
![\frac{\left(8+12\sqrt[2]{3}+18 + 9 \right)\left(8 - 12\sqrt[2]{3}+ 18 - 9\right)}{\sqrt[2]{3}} \frac{\left(8+12\sqrt[2]{3}+18 + 9 \right)\left(8 - 12\sqrt[2]{3}+ 18 - 9\right)}{\sqrt[2]{3}}](/latexrender/pictures/4dc2551835be4220388c45b56b2fd9f9.png) =
= ![\frac{\left(35 + 12\sqrt[2]{3}\right)-\left(17 - 12\sqrt[2]{3}\right) }{\sqrt[2]{3}} \frac{\left(35 + 12\sqrt[2]{3}\right)-\left(17 - 12\sqrt[2]{3}\right) }{\sqrt[2]{3}}](/latexrender/pictures/f02a543df354c80b3b4cd5734bf8654b.png)

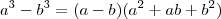
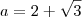
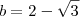



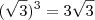 e não
e não 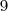 como você colocou, se você corrigir este errinho encontrará a resposta.
como você colocou, se você corrigir este errinho encontrará a resposta.
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)