UEL-PR triângulos

por **Kelvin Brayan** » Qui Abr 07, 2011 03:00

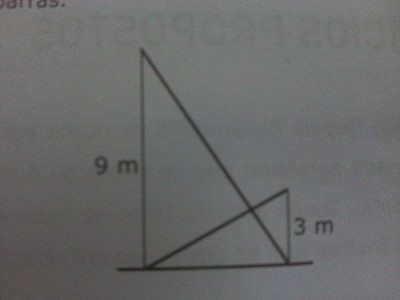
(UEL-PR) Após um tremor de terra, dois muros paralelos em uma rua de uma cidade ficaram ligeiramente abalados. Os moradores se reuniram e decidiram escorar os muros utilizando duas barras metálicas, como mostra a figura. Sabendo que os muros têm alturas de 9m e 3m, respectivamente, a que altura do nível do chão as duas barras se interceptam ? Despreze a espessura das barras

por **Fabricio dalla** » Qui Abr 07, 2011 16:14

a resposta e quanto ? 9/4!?

por **Kelvin Brayan** » Qui Abr 07, 2011 16:23

a resposta é 2,25m = 9/4 é isso mesmo ! como se resolve?

por **Fabricio dalla** » Qui Abr 07, 2011 17:39

a cara nao tem como so mostrando a imagem mas se tem q aplicar teorema de tales pra ver que eles sao semelhantes achar a razao entre eles e aplicar a propriedade de semelhança de areas ai traçar as alturas relativas a cada triangulo onde vc vai perceber outro caso de semelhança onde la vc acha a resposta

por **Elcioschin** » Qui Abr 07, 2011 19:04

Existe uma solução muito simples usando Geometria Analítica:

Seja um sistema xOy com a origem no pé do muo mais alto e o chão no eixo X
Seja d a distãncia entre os dois muros

1) Equação da reta suporte da barra menor, cujo coeficiente angular vale 3/d ----> y = (3/d)*x

2) Idem da reta suporte da barra maior, com coeficiente angular -9/d ----> y = (-9/d)*x + 9

No ponto de cruzamento as duas abcissas (x) e ordenadas (y) são iguais: (3/d)*x = (-9/d)*x + 9 ----> (12/d)*x = 9 ----> x = (3/4)*d

y = (3/d)*x ----> y = (3/d)*(3/4)*d ----> y = 9/4

por **Fabricio dalla** » Sex Abr 08, 2011 00:08

uahsuasauhs irado !! mas ai se apelo tbm kkk

por **FilipeCaceres** » Sex Abr 08, 2011 00:34

: relação_triangulo.GIF (2.19 KiB) Exibido 27631 vezes

Vou postar minha solução também.
Fazendo semelhando temos,
$\frac{3}{a+b}=\frac{x}{b}$ (i)

$\frac{9}{a+b}=\frac{x}{a}$ (ii)

Dividindo uma da outra encontramos
b=3a