Análise combinatória, Probabilidade e Noções de estatística

[mateusmarques]

1. Leis de De Morgan - Dados dois conjuntos A e B, mostre que:
(a) (AUB)^C = A^C?B^C
(b) (A?B)^C = A^C U B^C

2. Seja ?={1,0}3 . Este conjunto pode ser visto como o conjunto de resultados de três lançamentos de uma moeda (0 denota coroa e 1 denota cara). Defina os conjuntos
A={? s1, s2, s3???: s2=1} e B={? s1, s2, s3???: s1?s2?s3=2} . Liste os elementos de cada
um dos conjuntos a seguir: ? , A, B, A^C , B^C , A?B , A?B , A \ B e B \ A .

[FilipeCaceres]

Eu sei que figura não é o suficiente para uma demonstração, mas vou colocar para uma melhor visualização da demonstração.
a)

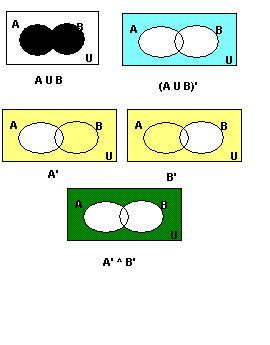
Morgan.GIF (3.87 KiB) Exibido 4660 vezes

Entenda x' como complemento de x.

Para (b) é semelhante
Abraço.

[benni]

Ex 1-lei de De morgan (anexo).
Ex.2 - A={(1,1,0);(0,1,0);(1,0,0)} s2=1
B = {(0,0,1);(0,1,0);(0,0,0)} s1+s2+s3= 2
agora é mostrar no diagrama de Venn, como já demonstrou o colega(não esta completo)