Boa noite, meu professor passou uma folha de exercicios sem explicar, estou com uma duvida que pode ate ser muito boba, mas quem puder, por favor me ajude.
lim x->3 [2x-f(x)]=6 gostaria de saber se esta certo calcular direto 2.3-f(x)=6 = 6-6=0 ou se posso usar operação inversa e fazer dessa forma 2.3- f(x)=6
=6- f(x)=6
F(x)=6+6= 12 Bem, gostaria de saber qual forma ta certa, porque a prova é Quinta e acho que estou fazendo besteira no trabalho, so me ensinem a forma de calcular, por favor!!! Obrigada.




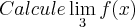
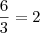
 ai multipliquei cruzado e fiz
ai multipliquei cruzado e fiz 
 ai eu fiz
ai eu fiz  Quero saber se estou calculando da forma certa, e se não estiver como devo calcular esse tipo de conta, desde ja muito obrigada^^
Quero saber se estou calculando da forma certa, e se não estiver como devo calcular esse tipo de conta, desde ja muito obrigada^^
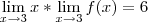



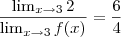

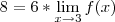


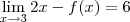



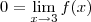

 .
.



