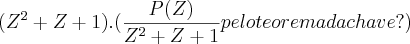por Fabricio dalla » Ter Abr 05, 2011 17:19
por Fabricio dalla » Ter Abr 05, 2011 17:19
(UFES) o numero complexo
![{Z}_{1}=\frac{-1}{2}+i\frac{\sqrt[2]{3}}{2} e uma das raizes do polinomio
[tex]
P(Z)={Z}^{4}+2{Z}^{3}+{Z}^{2}-1 {Z}_{1}=\frac{-1}{2}+i\frac{\sqrt[2]{3}}{2} e uma das raizes do polinomio
[tex]
P(Z)={Z}^{4}+2{Z}^{3}+{Z}^{2}-1](/latexrender/pictures/b2b5cdd2c87d0613ff1d8a7e2723fbd3.png)
a)Encontre outra raiz complexa não real de P(Z)
b)escreva P(Z)como produto de dois polinomios com coeficiente reais[/tex]
o que devo fazer
na alternativa a) quando ele fala outra raiz complexa não real de P(Z) ele se refere a um numero complexo imaginario puro ou eu devo colocar so o conjugado de z1 como resposta ?
b)com essas duas raizes complexas eu desço o grau do polinomio ate grau 2 ai escrevo que P(Z)=P(Z) baixado 2grausX o produto de (Z-Z1).(Z-Z2) onde Z2 e o conjugado de Z1?
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Elcioschin » Ter Abr 05, 2011 19:04
por Elcioschin » Ter Abr 05, 2011 19:04
Se - 1/2 + i*V3/2 é uma raiz complexa, outra raiz, obrigatoriamente complexa é -1/2 - i*V3/2
[z - (-1/2 + i*V3/2)]*[z - (-1/2 - i*V3/2)] = [ (z + 1/2) + i*V3/2]*[(z + 1/2) - i*V3/2] = (z + 1/2)² - (i*V3/2)² = (z² + z + 1/4) - (- 3/4) = z² + z + 1
Divida agora o polinômio original (do 4º grau) por x² + x + 1 e encontre outro polinômio do 2º grau .
Igualando este último a zero você encontra as outras duas raízes.
Editado pela última vez por
Elcioschin em Qua Abr 06, 2011 09:25, em um total de 1 vez.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Fabricio dalla » Ter Abr 05, 2011 23:12
por Fabricio dalla » Ter Abr 05, 2011 23:12
ta ai pra responder a letra B seria P(Z)=
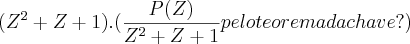
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Elcioschin » Qua Abr 06, 2011 09:23
por Elcioschin » Qua Abr 06, 2011 09:23
Sim: o outro polinômio é (z² + 1) ----> Duas raízes imaginárias z = i
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [TRIGONOMETRIA] preciso de orientaçao para resoluçao
por Fabricio dalla » Qua Jun 13, 2012 17:05
- 1 Respostas
- 1902 Exibições
- Última mensagem por LuizAquino

Qua Jun 13, 2012 20:52
Trigonometria
-
- Boa tarde preciso de uma orientação neste exercicio
por valdinei » Qua Nov 16, 2016 18:19
- 1 Respostas
- 3624 Exibições
- Última mensagem por adauto martins

Sex Nov 18, 2016 16:41
Cálculo: Limites, Derivadas e Integrais
-
- preciso da Fórmula para resolver
por Dankaerte » Qui Ago 27, 2009 14:36
- 1 Respostas
- 5146 Exibições
- Última mensagem por Molina

Qui Ago 27, 2009 17:50
Estatística
-
- Preciso de um ponto para me guiar!
por acekaze » Sex Jun 03, 2011 07:23
- 1 Respostas
- 1623 Exibições
- Última mensagem por Neperiano

Sex Out 28, 2011 15:47
Estatística
-
- Preciso de ajuda para ver se esta correto
por arima » Qui Fev 10, 2011 16:59
- 2 Respostas
- 2487 Exibições
- Última mensagem por arima

Sáb Fev 12, 2011 11:16
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![{Z}_{1}=\frac{-1}{2}+i\frac{\sqrt[2]{3}}{2} e uma das raizes do polinomio
[tex]
P(Z)={Z}^{4}+2{Z}^{3}+{Z}^{2}-1 {Z}_{1}=\frac{-1}{2}+i\frac{\sqrt[2]{3}}{2} e uma das raizes do polinomio
[tex]
P(Z)={Z}^{4}+2{Z}^{3}+{Z}^{2}-1](/latexrender/pictures/b2b5cdd2c87d0613ff1d8a7e2723fbd3.png)