 por AlbertoAM » Ter Abr 05, 2011 14:44
por AlbertoAM » Ter Abr 05, 2011 14:44
Eu fiz até aqui:
http://img148.imageshack.us/i/continuidade.jpg/Mas na parte de verificar se os resultados obtidos contradizem a álgebra dos limites eu não to conseguindo fazer.Poderia me ajudar por favor.
Com relação ao exercício 243, a imagem ficaria Im=]-?,-3] U ]0,?[ ?
Poderia verificar também se as resoluções dos exercícios 244, 245 e 246 estão corretas.
-
AlbertoAM
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Qui Nov 11, 2010 15:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por LuizAquino » Ter Abr 05, 2011 19:29
por LuizAquino » Ter Abr 05, 2011 19:29
Mas na parte de verificar se os resultados obtidos contradizem a álgebra dos limites eu não to conseguindo fazer
Você deve analisar se é verdadeiro dizer nesses casos que

e que

.
Com relação ao exercício 243, a imagem ficaria Im=]-?, -3] U ]0, +?[ ?
Sim.
Poderia verificar também se as resoluções dos exercícios 244, 245 e 246 estão corretas.
Reveja a imagem da função no exercício 246.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por AlbertoAM » Ter Abr 05, 2011 20:53
por AlbertoAM » Ter Abr 05, 2011 20:53
De acordo com a álgebra dos limites:

No exercício 247 temos que
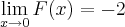
Mas como não existe

e nem
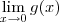
O resultado obtido contraria a álgebra dos limites.
No outro caso:
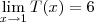
Mas como existe

e nem
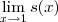
O resultado obtido também contraria a álgebra dos limtes.
Agora fiquei curioso, porque eles contrariam a álgebra dos limites?
A imagem da função do exercício 246 então ficaria Im=]-?,6[ ?
-
AlbertoAM
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Qui Nov 11, 2010 15:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por LuizAquino » Ter Abr 05, 2011 21:15
por LuizAquino » Ter Abr 05, 2011 21:15
Na verdade, esses limites não "contrariam" as regras.
O que acontece é que antes de aplicar as regras devemos observar se os limites de cada parcela (ou de cada fator) existem. Se um deles não existe, então a regra não pode ser aplicada.
O problema desse exercício está no fato de tentar aplicar as regras em limites que não existem.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por AlbertoAM » Ter Abr 05, 2011 21:27
por AlbertoAM » Ter Abr 05, 2011 21:27
Entendi cara, Muito Obrigado pela explicação.
-
AlbertoAM
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Qui Nov 11, 2010 15:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por leochacon » Qua Abr 06, 2011 00:12
por leochacon » Qua Abr 06, 2011 00:12
Será que alguem pode me ajudar a fazer esse exercício?
Questão 7: Determinado produtor vende 50 litros de leite para uma empresa de laticínio por dia ao
valor de R$ 1,20 o litro. Para aumentar sua produção e venda para a empresa, esse decidiu que
diminuiria 1 centavo no preço de cada litro de leite vendido para cada unidade a mais que fosse vendido.
Sabendo-se que o custo de produção de cada litro de leite é igual a R$ 0,30, determine
a) A função que representa o valor da receita diária R em função da quantidade x a mais produzida.
b) A função que representa o valor do custo diário C em função da quantidade x a mais produzida.
c) A função que representa o valor do lucro diário L em função da quantidade x a mais produzida.
d) A quantidade de litros que o produtor deverá vender para ter lucro máximo.
e) Faça uma tabela cuja primeira coluna tenha a quantidade de litros de leite vendidos pelo
produtor, a segunda coluna contenha a Receita bruta diária, a terceira coluna contenha o Custo
diário e a última coluna contenha o lucro diário. Faça a tabela até que o lucro diário se torne
inferior ao lucro obtido quando ele vendia apenas 50 litros de leite.
Quantidade de litros vendidos Receita Bruta (R$) Custo (R$) Lucro (R$)
50 60,00 15,00 45,00
51 60,69 15,30 45,39
52 61,36 15,60 45,76
.................... .................... .................... ....................
Continue.... Continue.... Continue.... Continue....
.................... .................... .................... ....................
f) Use a tabela do item anterior para esboçar os gráficos (em um mesmo plano cartesiano) os
gráficos da Receita Bruta, do Custo e do Lucro diários.
-
leochacon
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Out 27, 2010 16:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Gestão do Agronegócio
- Andamento: cursando
 por LuizAquino » Qua Abr 06, 2011 10:33
por LuizAquino » Qua Abr 06, 2011 10:33
Olá leochacon,
Por motivo de organização, não use tópicos já existentes para enviar novos exercícios.
Crie um novo tópico para cada novo exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Continuidade
por guilherme5088 » Sáb Out 12, 2019 15:31
- 1 Respostas
- 5333 Exibições
- Última mensagem por adauto martins

Ter Out 15, 2019 23:11
Cálculo: Limites, Derivadas e Integrais
-
- Continuidade
por MCordeiro » Qui Jul 16, 2020 19:11
- 1 Respostas
- 3540 Exibições
- Última mensagem por adauto martins

Qua Out 14, 2020 12:00
Cálculo: Limites, Derivadas e Integrais
-
- Exercicio de Continuidade
por PeIdInHu » Qua Jul 14, 2010 21:04
- 2 Respostas
- 3065 Exibições
- Última mensagem por PeIdInHu

Qui Jul 15, 2010 01:03
Cálculo: Limites, Derivadas e Integrais
-
- Limite Continuidade
por Claudin » Sáb Out 01, 2011 11:33
- 10 Respostas
- 5808 Exibições
- Última mensagem por Claudin

Seg Out 03, 2011 10:37
Cálculo: Limites, Derivadas e Integrais
-
- [Continuidade] Demonstração
por Aliocha Karamazov » Sáb Out 29, 2011 14:20
- 4 Respostas
- 3138 Exibições
- Última mensagem por Aliocha Karamazov

Sáb Out 29, 2011 21:11
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


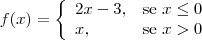

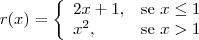
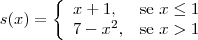



 e que
e que  .
.
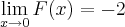
 e nem
e nem 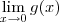
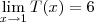
 e nem
e nem 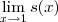

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
