 por Caeros » Seg Abr 04, 2011 13:09
por Caeros » Seg Abr 04, 2011 13:09
Olá caros(as) me ajudem a compreender esta questão:
Seja G =
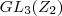
o grupo linear, onde
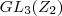
= {
![A\:\in\:{M}_{3} ({Z}_{2} )\::\:det(A)\:\neq\:[0] A\:\in\:{M}_{3} ({Z}_{2} )\::\:det(A)\:\neq\:[0]](/latexrender/pictures/b8c7137a39fa94e1bfae8dd8ee8e8934.png)
}
e
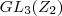
o conjunto das matrizes sobre

de ordem 3: Mostre que IGI = 168:
Sei que é necessário saber o número de matrizes invertíveis, pelo menos acho que este é um caminho, mas não consegui. Ajuda.


-
Caeros
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Seg Mai 25, 2009 19:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Seg Abr 04, 2011 22:23
por MarceloFantini » Seg Abr 04, 2011 22:23
Caeros, você faz bacharelado em matemática?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Caeros » Ter Abr 05, 2011 09:31
por Caeros » Ter Abr 05, 2011 09:31
Olá Fantini;
Eu estou estudando para Licenciatura em Matemática, porém a grade do meu curso é um pouco pesada e em nível de bacharel, por isso estou sempre recorrendo ao site. Grato. Caetano

-
Caeros
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Seg Mai 25, 2009 19:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Ter Abr 05, 2011 10:41
por LuizAquino » Ter Abr 05, 2011 10:41
Olá Caeros,
Tenha a convicção que a sua grade de licenciado não está "pesada" por estar próxima da grade do bacharel. Ela simplesmente está no nível que deve estar!
Não esqueça que um Licenciado em Matemática deve ser preparado para dar aula em todos os níveis da educação, isto é, do ensino fundamental ao superior.
É um equívoco comum entre os graduandos em Licenciatura em Matemática achar que o curso deve ser voltado para formar apenas professores de ensino fundamental e médio.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Algebra linear] Matrizes
por Souo » Sex Ago 19, 2016 19:40
- 0 Respostas
- 2907 Exibições
- Última mensagem por Souo

Sex Ago 19, 2016 19:40
Álgebra Linear
-
- [Algebra linear] Matrizes
por Souo » Sex Ago 19, 2016 19:42
- 0 Respostas
- 3032 Exibições
- Última mensagem por Souo

Sex Ago 19, 2016 19:42
Álgebra Linear
-
- [Álgebra linear] Igualdade de matrizes
por Suellem Albuquerque » Sex Mar 28, 2014 15:23
- 2 Respostas
- 3094 Exibições
- Última mensagem por Suellem Albuquerque

Seg Mar 31, 2014 11:46
Álgebra Linear
-
- Grupos e Subgrupos
por Renato_RJ » Sex Jan 21, 2011 13:18
- 4 Respostas
- 4786 Exibições
- Última mensagem por Renato_RJ

Sex Jan 21, 2011 16:39
Álgebra Elementar
-
- Teoria de grupos
por Luiz Augusto Prado » Seg Mai 30, 2011 21:37
- 1 Respostas
- 1394 Exibições
- Última mensagem por Luiz Augusto Prado

Ter Mai 31, 2011 19:21
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
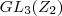 o grupo linear, onde
o grupo linear, onde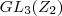 = {
= {![A\:\in\:{M}_{3} ({Z}_{2} )\::\:det(A)\:\neq\:[0] A\:\in\:{M}_{3} ({Z}_{2} )\::\:det(A)\:\neq\:[0]](/latexrender/pictures/b8c7137a39fa94e1bfae8dd8ee8e8934.png) }
}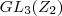 o conjunto das matrizes sobre
o conjunto das matrizes sobre  de ordem 3: Mostre que IGI = 168:
de ordem 3: Mostre que IGI = 168:
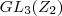 o grupo linear, onde
o grupo linear, onde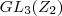 = {
= {![A\:\in\:{M}_{3} ({Z}_{2} )\::\:det(A)\:\neq\:[0] A\:\in\:{M}_{3} ({Z}_{2} )\::\:det(A)\:\neq\:[0]](/latexrender/pictures/b8c7137a39fa94e1bfae8dd8ee8e8934.png) }
}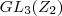 o conjunto das matrizes sobre
o conjunto das matrizes sobre  de ordem 3: Mostre que IGI = 168:
de ordem 3: Mostre que IGI = 168:



