 por Caeros » Seg Abr 04, 2011 13:09
por Caeros » Seg Abr 04, 2011 13:09
Olá caros(as) me ajudem a compreender esta questão:
Seja G =
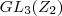
o grupo linear, onde
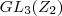
= {
![A\:\in\:{M}_{3} ({Z}_{2} )\::\:det(A)\:\neq\:[0] A\:\in\:{M}_{3} ({Z}_{2} )\::\:det(A)\:\neq\:[0]](/latexrender/pictures/b8c7137a39fa94e1bfae8dd8ee8e8934.png)
}
e
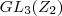
o conjunto das matrizes sobre

de ordem 3: Mostre que IGI = 168:
Sei que é necessário saber o número de matrizes invertíveis, pelo menos acho que este é um caminho, mas não consegui. Ajuda.


-
Caeros
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Seg Mai 25, 2009 19:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Seg Abr 04, 2011 22:23
por MarceloFantini » Seg Abr 04, 2011 22:23
Caeros, você faz bacharelado em matemática?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Caeros » Ter Abr 05, 2011 09:31
por Caeros » Ter Abr 05, 2011 09:31
Olá Fantini;
Eu estou estudando para Licenciatura em Matemática, porém a grade do meu curso é um pouco pesada e em nível de bacharel, por isso estou sempre recorrendo ao site. Grato. Caetano

-
Caeros
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Seg Mai 25, 2009 19:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Ter Abr 05, 2011 10:41
por LuizAquino » Ter Abr 05, 2011 10:41
Olá Caeros,
Tenha a convicção que a sua grade de licenciado não está "pesada" por estar próxima da grade do bacharel. Ela simplesmente está no nível que deve estar!
Não esqueça que um Licenciado em Matemática deve ser preparado para dar aula em todos os níveis da educação, isto é, do ensino fundamental ao superior.
É um equívoco comum entre os graduandos em Licenciatura em Matemática achar que o curso deve ser voltado para formar apenas professores de ensino fundamental e médio.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Algebra linear] Matrizes
por Souo » Sex Ago 19, 2016 19:40
- 0 Respostas
- 2907 Exibições
- Última mensagem por Souo

Sex Ago 19, 2016 19:40
Álgebra Linear
-
- [Algebra linear] Matrizes
por Souo » Sex Ago 19, 2016 19:42
- 0 Respostas
- 3032 Exibições
- Última mensagem por Souo

Sex Ago 19, 2016 19:42
Álgebra Linear
-
- [Álgebra linear] Igualdade de matrizes
por Suellem Albuquerque » Sex Mar 28, 2014 15:23
- 2 Respostas
- 3094 Exibições
- Última mensagem por Suellem Albuquerque

Seg Mar 31, 2014 11:46
Álgebra Linear
-
- Grupos e Subgrupos
por Renato_RJ » Sex Jan 21, 2011 13:18
- 4 Respostas
- 4786 Exibições
- Última mensagem por Renato_RJ

Sex Jan 21, 2011 16:39
Álgebra Elementar
-
- Teoria de grupos
por Luiz Augusto Prado » Seg Mai 30, 2011 21:37
- 1 Respostas
- 1394 Exibições
- Última mensagem por Luiz Augusto Prado

Ter Mai 31, 2011 19:21
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
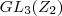 o grupo linear, onde
o grupo linear, onde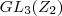 = {
= {![A\:\in\:{M}_{3} ({Z}_{2} )\::\:det(A)\:\neq\:[0] A\:\in\:{M}_{3} ({Z}_{2} )\::\:det(A)\:\neq\:[0]](/latexrender/pictures/b8c7137a39fa94e1bfae8dd8ee8e8934.png) }
}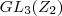 o conjunto das matrizes sobre
o conjunto das matrizes sobre  de ordem 3: Mostre que IGI = 168:
de ordem 3: Mostre que IGI = 168:
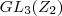 o grupo linear, onde
o grupo linear, onde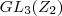 = {
= {![A\:\in\:{M}_{3} ({Z}_{2} )\::\:det(A)\:\neq\:[0] A\:\in\:{M}_{3} ({Z}_{2} )\::\:det(A)\:\neq\:[0]](/latexrender/pictures/b8c7137a39fa94e1bfae8dd8ee8e8934.png) }
}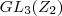 o conjunto das matrizes sobre
o conjunto das matrizes sobre  de ordem 3: Mostre que IGI = 168:
de ordem 3: Mostre que IGI = 168:








