Um trem percorreu 200km em um certo tempo. Se tivesse aumentado sua velocidade em 10km/h, teria percorrido essa distância em 1 hora menos. Determinar a velocidade do trem, em km/h.
Em todas as minhas tentantivas de equacionar o problema eu chegava na seguinte equação:
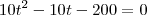
mas os resultados são 5 e -4
Esses foram os meus passos
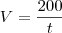
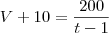
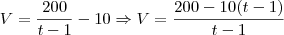
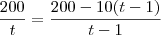
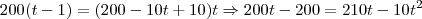
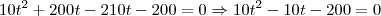
Tentando por regra de três eu me deparei com:
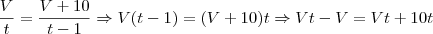

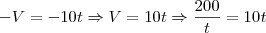
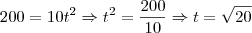
Uffa! Levando em consideração que eu possa ter errado alguma coisa ao passar para o fórum é mais ou menos isso

Ah! o resultado deveria ser 40km/h



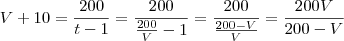
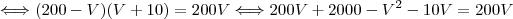
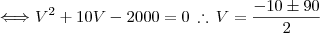
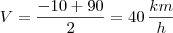



 a resposta ficaria
a resposta ficaria 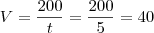 .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)