Maligno escreveu:Tem-se um onibus, nele há 7 garotas, cada garota têm 7 mochilas, dentro de cada mochila há 7 gatos grandes, cada gato grande tem 7 gatos pequenos. Considerando que cada gato tem 4 pernas. Quantas pernas há dentro do onibus?
Boa tarde, Maligno.
Se levarmos ao pé da letra esse exercício, teríamos a seguinte conta:
7 garotas * 2 pernas = 14 pernas
1 garota = 7 mochilas * 7 gatos = 49 gatos grandes * 7 gatos pequenos = 343
7 garotas = 343 * 7 = 2401
2401 * 4 pernas = 9604 pernas
9604 pernas + 14 pernas =
9618 pernas to total.
-----------------------------------------------------------------
Ou então, há quem fale que animais tem patas e nao pernas. Então so teria as
14 pernas das garotas.
-----------------------------------------------------------------
Não tive tempo de revisar as contas.
Problemas deste tipo realmente dão um nó na cabeça.
Acho que dava pra resolver o lance dos gatos usando exponencial:

e somar com as pernas das garotas.

Aguardo confirmação
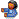



 e somar com as pernas das garotas.
e somar com as pernas das garotas. Aguardo confirmação
Aguardo confirmação 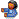





 , certo? Aproveitei agora para experimentar o LaTeX...
, certo? Aproveitei agora para experimentar o LaTeX... 









 .
.



