 por ronneysantos » Qui Mar 31, 2011 11:31
por ronneysantos » Qui Mar 31, 2011 11:31
Srs,
Segue em mais um obstáculo que não consegui resolver. Partindo do raciocício do exercício anterior cheguei a seguinte solução:
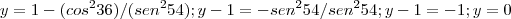
Entretanto diferente do gabarito:
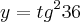
Srs, poderiam apontar o meu erro?
Obrigado
-
ronneysantos
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Dom Mar 27, 2011 20:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Elcioschin » Qui Mar 31, 2011 12:48
por Elcioschin » Qui Mar 31, 2011 12:48
QUAL exercício anterior?
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por ronneysantos » Qui Mar 31, 2011 13:41
por ronneysantos » Qui Mar 31, 2011 13:41
"Problema Elementar de Cossenos" em Trigonometria.
viewtopic.php?f=109&t=4233Abs,
Ronney
-
ronneysantos
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Dom Mar 27, 2011 20:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por ronneysantos » Qui Mar 31, 2011 14:08
por ronneysantos » Qui Mar 31, 2011 14:08
Srs,
Acabei de ver o meu erro. "Não existe passar o numero 1 para o outro lado" (no primeiro passo da questão). Putz, foi mal mesmo - vacilo total.
Dessa forma trilhei um caminho diferente onde, pelo qual, consegui resolver. Segue os passos adotados:

; Aplicando a relação Fundamental:

; fica assim:

; Aplicando a dica do exercicio anterior; fica assim:

; Aplicando:

; fica assim:
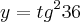
=> RESOLVIDO!
Muito Obrigado a todos e desculpem o meu vacilo.
-
ronneysantos
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Dom Mar 27, 2011 20:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema Elementar de Cossenos
por ronneysantos » Dom Mar 27, 2011 21:05
- 6 Respostas
- 3713 Exibições
- Última mensagem por ronneysantos

Qui Mar 31, 2011 10:59
Trigonometria
-
- [Algebra Elementar] Dúvida em resposta do problema
por marco70 » Ter Jun 14, 2016 14:52
- 0 Respostas
- 1837 Exibições
- Última mensagem por marco70

Ter Jun 14, 2016 14:52
Álgebra Elementar
-
- Aritmética Elementar
por Abelardo » Seg Mar 07, 2011 00:36
- 7 Respostas
- 7331 Exibições
- Última mensagem por LuizAquino

Dom Mai 08, 2011 17:29
Álgebra Elementar
-
- Álgebra Elementar
por Abelardo » Seg Mar 14, 2011 18:09
- 1 Respostas
- 2312 Exibições
- Última mensagem por LuizAquino

Seg Mar 14, 2011 18:21
Álgebra Elementar
-
- Álgebra Elementar
por Thiago Josep » Sex Set 05, 2014 15:32
- 1 Respostas
- 2664 Exibições
- Última mensagem por DanielFerreira

Qui Jan 01, 2015 22:22
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
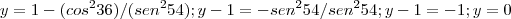
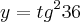

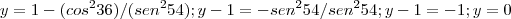
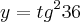



 ; Aplicando a relação Fundamental:
; Aplicando a relação Fundamental:  ; fica assim:
; fica assim: ; Aplicando a dica do exercicio anterior; fica assim:
; Aplicando a dica do exercicio anterior; fica assim: ; Aplicando:
; Aplicando:  ; fica assim:
; fica assim: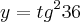 => RESOLVIDO!
=> RESOLVIDO!