50) Uma das raízes complexas da equação x³ + 3x² + 8x - 6 = 0 é:
resp:
![1+i\sqrt[]{3} 1+i\sqrt[]{3}](/latexrender/pictures/866000504e9ad5234c1201a8c652df3f.png)
Eu tentei assim:
x³ + 3x² + 8x - 6 = 0
x [x (x - 3) + 8] - 6 = 0 Achei que (x - 3) era uma das raízes, usei o método "Briot-Ruffini " aquele que parece uma divisão no final tem que restar zero. Não dá zero.
Tentei também (a + b)(a² + 2ab + b²) e não foi. ai desisti e chutei essa e um monte das outras, mesmo assim fiz 26 pontos faltaram só 4 pontos em matemática prá passar foi quase.


![1+i\sqrt[]{5} 1+i\sqrt[]{5}](/latexrender/pictures/631d106da9f9fabf19766ed612afecaf.png) . Independente disso vc me ensinou como resolver, é só ir pelas alternativas e usar a relação de Girard. Desculpe e obrigado.
. Independente disso vc me ensinou como resolver, é só ir pelas alternativas e usar a relação de Girard. Desculpe e obrigado.![2+i\sqrt[]{3} 2+i\sqrt[]{3}](/latexrender/pictures/230f049e37a3814fb493cc84752a6376.png) deu -1. A (d) que é a certa deu 1 também e a (e) deu -1. Se eu usasse a relação de Girard logo na (a) já encontraria a raiz, só que a resposta taria errada por não ser a outra raiz (complexa) procurada. Tem mais alguma coisa que falta fazer pra confirmar se a raiz é a procurada?
deu -1. A (d) que é a certa deu 1 também e a (e) deu -1. Se eu usasse a relação de Girard logo na (a) já encontraria a raiz, só que a resposta taria errada por não ser a outra raiz (complexa) procurada. Tem mais alguma coisa que falta fazer pra confirmar se a raiz é a procurada? de coeficientes reais inteiros, admite uma raiz racional
de coeficientes reais inteiros, admite uma raiz racional 
 e p,q sao primos entre si, entao p é divisor de
e p,q sao primos entre si, entao p é divisor de 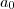 e q é divisor de
e q é divisor de  .
.
 e
e 
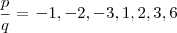

 e
e
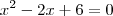
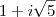


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
