 por fernandocez » Sex Mar 25, 2011 13:12
por fernandocez » Sex Mar 25, 2011 13:12
Caros amigos do Forum, vcs tem me ajudado muito, já aprendi muita coisa desde que conheci esse forum, já divulguei prá vários amigos que precisa de uma ajuda em Matemática. Mas vamos a mais uma questão que não consigo resolver.
45) O conjunto solução da equação
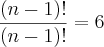
é:
resp: S = {2}
Eu fiz assim.
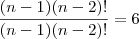
depois distribui

Obs. esse A que tá aparecendo é defeito do programa.
Daqui eu não consigo prosseguir, se é que tô fazendo certo.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por Molina » Sex Mar 25, 2011 14:09
por Molina » Sex Mar 25, 2011 14:09
Boa tarde, Fernando.
Confirme se você escreveu os fatoriais correto, pois se você for ver, o numerador e o denominador da fração estão iguais, e isso daria 1. Mas 1 nunca será igual a 6.
Aguardo sua confirmação.
Quando a esse  que aparece no meio de sua fórmula do LaTeX, é porque você está utilizando o 2 sobrescrito (²) [normalmente acessado do telcado por alt + 2]. O LaTeX não consegue ler esse caracter. Para fazer expoente utilize o acento circunflexo (^)
Seu código correto, ficaria assim:
- Código: Selecionar todos
[tex]\frac{(n^2- 2n-n+2)!}{(n^2- 2n-n+2)!}=6[/tex]

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por profmatematica » Sex Mar 25, 2011 14:18
por profmatematica » Sex Mar 25, 2011 14:18
Ola amigo acredito que seu enunciado seja assim (n+1)! / (n-1)! =6 se assim for teremos (n+1).(n).(n-1)! / (n-1)! = 6 entao cortando os termos semelhantes (n-1)! Teremos (n+1).(n)=6 resolvendo teremos n ao quadrado + n -6=0 resolva dai tu vai achar delta =25 n'=2 n"=- 3 resposta indesejada negativa. Entao n=2 ok?
-
profmatematica
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Sex Ago 27, 2010 13:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por fernandocez » Sex Mar 25, 2011 21:45
por fernandocez » Sex Mar 25, 2011 21:45
Molina escreveu:Boa tarde, Fernando.
Confirme se você escreveu os fatoriais correto, pois se você for ver, o numerador e o denominador da fração estão iguais, e isso daria 1. Mas 1 nunca será igual a 6.
Aguardo sua confirmação.
Quando a esse  que aparece no meio de sua fórmula do LaTeX, é porque você está utilizando o 2 sobrescrito (²) [normalmente acessado do telcado por alt + 2]. O LaTeX não consegue ler esse caracter. Para fazer expoente utilize o acento circunflexo (^)
Seu código correto, ficaria assim:
- Código: Selecionar todos
[tex]\frac{(n^2- 2n-n+2)!}{(n^2- 2n-n+2)!}=6[/tex]

Oi Molina, está da mesma forma que escrevi a expressão, eu até pensei assim também, que daria um mas por ser fatorial eu pensei que tinha alguma coisa a mais que eu não tava percebendo. Tipo, zero fatorial é igual a 1. Então quer dizer que a questão foi anulada. Sobre os caracteres é realmente eu usei o sobrescrito, obrigado pelas dicas.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por fernandocez » Sex Mar 25, 2011 21:53
por fernandocez » Sex Mar 25, 2011 21:53
profmatematica escreveu:Ola amigo acredito que seu enunciado seja assim (n+1)! / (n-1)! =6 se assim for teremos (n+1).(n).(n-1)! / (n-1)! = 6 entao cortando os termos semelhantes (n-1)! Teremos (n+1).(n)=6 resolvendo teremos n ao quadrado + n -6=0 resolva dai tu vai achar delta =25 n'=2 n"=- 3 resposta indesejada negativa. Entao n=2 ok?
Oi amigo, como disse acima essa questão deve ter sido anulada, mas valeu o seu desenvolvimento da questão porque acabei aprendendo, se aparecer uma questão parecida eu já sei desenvolver. Obrigado.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão prova concurso
por fernandocez » Sáb Fev 26, 2011 19:10
- 6 Respostas
- 3560 Exibições
- Última mensagem por fernandocez

Sáb Fev 26, 2011 22:29
Geometria Plana
-
- Questão prova concurso
por fernandocez » Sáb Fev 26, 2011 23:27
- 3 Respostas
- 2503 Exibições
- Última mensagem por fernandocez

Dom Fev 27, 2011 10:33
Funções
-
- Questão prova concurso (sen e cos)
por fernandocez » Qua Mar 02, 2011 11:26
- 13 Respostas
- 9289 Exibições
- Última mensagem por fernandocez

Dom Mar 13, 2011 12:18
Trigonometria
-
- Questão prova concurso com Latitude
por fernandocez » Sáb Fev 26, 2011 23:38
- 2 Respostas
- 1824 Exibições
- Última mensagem por fernandocez

Qua Mar 02, 2011 11:27
Geometria Plana
-
- Questão prova concurso combinatória
por fernandocez » Ter Mar 01, 2011 12:35
- 2 Respostas
- 2676 Exibições
- Última mensagem por fernandocez

Qui Mar 03, 2011 22:47
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
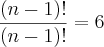 é:
é: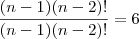
 Obs. esse A que tá aparecendo é defeito do programa.
Obs. esse A que tá aparecendo é defeito do programa.
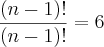 é:
é: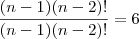
 Obs. esse A que tá aparecendo é defeito do programa.
Obs. esse A que tá aparecendo é defeito do programa.






