 por andersontricordiano » Qui Mar 24, 2011 16:57
por andersontricordiano » Qui Mar 24, 2011 16:57
Se log 2= a e log 3= b, calcule em função de a e b os seguintes logaritmos decimais:a) log 5
b)
![log\sqrt[5]{72} log\sqrt[5]{72}](/latexrender/pictures/c9dae4e1c71ff3ad2fe4030029f4e543.png)
c)log 500
Resposta:a) 1-a
b)
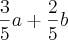
c) 3- a
Eu estou tentando resolver esse três calculo . Mas eu não estou conseguindo!
Obrigado quem resolver esse exercício!
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Qui Mar 24, 2011 17:23
por LuizAquino » Qui Mar 24, 2011 17:23
Dicas(i) log 5 = log (10/2)
(ii)
![\log \sqrt[5]{72} = \log 2^{\frac{3}{5}}\cdot 3^{\frac{2}{5}} \log \sqrt[5]{72} = \log 2^{\frac{3}{5}}\cdot 3^{\frac{2}{5}}](/latexrender/pictures/c70ea5f603c9e43d3a2baf9210bc56aa.png)
(iii) log 500 = log (1000/2)
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calcule em função de a e b os seguintes logaritmos decimais
por andersontricordiano » Qui Mar 24, 2011 16:55
- 3 Respostas
- 4425 Exibições
- Última mensagem por profmatematica

Sex Mar 25, 2011 12:17
Logaritmos
-
- Calcule em função o logaritmo.
por andersontricordiano » Sáb Abr 02, 2011 17:54
- 1 Respostas
- 1720 Exibições
- Última mensagem por Elcioschin

Sáb Abr 02, 2011 23:27
Logaritmos
-
- logaritmos em função de a e b
por crfsatisfaction » Seg Jul 25, 2011 22:00
- 1 Respostas
- 2368 Exibições
- Última mensagem por Molina

Seg Jul 25, 2011 23:51
Logaritmos
-
- Calcule a função que contem logaritmo
por andersontricordiano » Qui Mai 05, 2011 20:19
- 4 Respostas
- 2156 Exibições
- Última mensagem por andersontricordiano

Sex Mai 06, 2011 16:38
Funções
-
- Calcule a raiz da função do 1º grau?
por breno1323 » Ter Jun 05, 2012 11:44
- 3 Respostas
- 1758 Exibições
- Última mensagem por joaofonseca

Ter Jun 05, 2012 12:30
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![log\sqrt[5]{72} log\sqrt[5]{72}](/latexrender/pictures/c9dae4e1c71ff3ad2fe4030029f4e543.png)
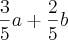

![log\sqrt[5]{72} log\sqrt[5]{72}](/latexrender/pictures/c9dae4e1c71ff3ad2fe4030029f4e543.png)
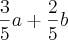

![\log \sqrt[5]{72} = \log 2^{\frac{3}{5}}\cdot 3^{\frac{2}{5}} \log \sqrt[5]{72} = \log 2^{\frac{3}{5}}\cdot 3^{\frac{2}{5}}](/latexrender/pictures/c70ea5f603c9e43d3a2baf9210bc56aa.png)


 .
.



