 por fernandocez » Qui Mar 24, 2011 10:20
por fernandocez » Qui Mar 24, 2011 10:20
Caro amigos matemáticos, venho com mais uma questão que não consegui resolver.
46) Em um curso de espanhol estudam vinte alunos, sendo doze rapazes e oito moças. O professor que formar uma equipe de quatro alunos para intercâmbio em outro país. O número de equipe de dois rapazer e duas moças que pode ser formadas é:
resp: 1848
Eu fiz.
C20,4 (comb. vinte quatro a quatro) = 4845
C12,4 = 495
C8,4 = 70
Somei as duas 495 + 70
Subtrair de 4845 - (495 + 70)
Fiz que nem uma outra, que era: formar equipe de três pessoas com pelo menos uma mulher. Eu fiz a combinação de todos e subtraí só os Homens.
Agora não deu certo, aonde que eu errei?
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por LuizAquino » Qui Mar 24, 2011 10:55
por LuizAquino » Qui Mar 24, 2011 10:55
ObservaçãoAo calcular

você está contando equipes:
(i) com apenas homens;
(ii) com apenas mulheres;
(iii) com 1 homem e 3 mulheres;
(iv) com 2 homens e 2 mulheres;
(v) com 3 homens e 1 mulher.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por fernandocez » Qui Mar 24, 2011 11:22
por fernandocez » Qui Mar 24, 2011 11:22
LuizAquino escreveu:ObservaçãoAo calcular

você está contando equipes:
(i) com apenas homens;
(ii) com apenas mulheres;
(iii) com 1 homem e 3 mulheres;
(iv) com 2 homens e 2 mulheres;
(v) com 3 homens e 1 mulher.
Oi Luiz, mas eu tenho que fazer a 1ª combinação contando todo mundo e depois eliminar os que não quero. Por exemplo: não quero, todos rapazes, todas moças e etc. No outro eu fiz a combinação com todo mundo e eliminei todos os homens juntos (foi isso que entendi). Tô meio perdido em combinação.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por LuizAquino » Qui Mar 24, 2011 11:36
por LuizAquino » Qui Mar 24, 2011 11:36
Número de equipes com:
(i) apenas homens:

.
(ii) apenas mulheres:

.
(iii) 1 homem e 3 mulheres:
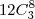
.
(iv) com 3 homens e 1 mulher:
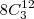
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por fernandocez » Qui Mar 24, 2011 12:06
por fernandocez » Qui Mar 24, 2011 12:06
LuizAquino escreveu:Número de equipes com:
(i) apenas homens:

.
(ii) apenas mulheres:

.
(iii) 1 homem e 3 mulheres:
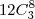
.
(iv) com 3 homens e 1 mulher:
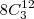
.
Luiz, eu entendi as combinações acima. Mas não consigo montar uma prá 2 homens e 2 mulheres. Teria que fazer separado e depois multiplicar?
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por LuizAquino » Qui Mar 24, 2011 12:19
por LuizAquino » Qui Mar 24, 2011 12:19
Número de equipes com 2 homens e 2 mulheres:
(i) Uma maneira de fazer:
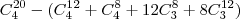
.
(ii) Outra maneira de fazer:

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por fernandocez » Qui Mar 24, 2011 12:23
por fernandocez » Qui Mar 24, 2011 12:23
LuizAquino escreveu:Número de equipes com 2 homens e 2 mulheres:
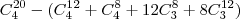
.
Essa eu nunca ia acertar. E coisa difícil esse negócio de combinação. E deve cair pelo menos uma assim na prova do estado RJ que vou fazer domingo. Obrigado.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão prova concurso
por fernandocez » Sáb Fev 26, 2011 19:10
- 6 Respostas
- 3550 Exibições
- Última mensagem por fernandocez

Sáb Fev 26, 2011 22:29
Geometria Plana
-
- Questão prova concurso
por fernandocez » Sáb Fev 26, 2011 23:27
- 3 Respostas
- 2497 Exibições
- Última mensagem por fernandocez

Dom Fev 27, 2011 10:33
Funções
-
- Questão prova concurso (sen e cos)
por fernandocez » Qua Mar 02, 2011 11:26
- 13 Respostas
- 9268 Exibições
- Última mensagem por fernandocez

Dom Mar 13, 2011 12:18
Trigonometria
-
- Dúvida Análise Comb.
por RJ1572 » Qua Mai 19, 2010 12:12
- 1 Respostas
- 1671 Exibições
- Última mensagem por MarceloFantini

Qua Mai 19, 2010 15:09
Estatística
-
- análise comb com cargos
por adrianosaldanha » Qui Out 20, 2011 17:03
- 1 Respostas
- 1434 Exibições
- Última mensagem por Neperiano

Qui Out 20, 2011 17:14
Sequências
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 você está contando equipes:
você está contando equipes:
 .
. .
.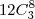 .
.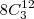 .
.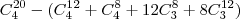 .
. .
.