 por johnlaw » Dom Mar 20, 2011 17:53
por johnlaw » Dom Mar 20, 2011 17:53
Olá pessoal,
Resolvi a seguinte inequação:
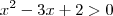
e obtive os dois resultados:
x1 = 2
x2 = 1
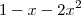
, essa com:
x1 = -1
x2 =

Mas não compreendo o que isso significa! Como fica esses intervalos na reta dos reais ?
Valeu!
-
johnlaw
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Ago 06, 2010 13:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática Licenciatura
- Andamento: cursando
 por LuizAquino » Dom Mar 20, 2011 18:35
por LuizAquino » Dom Mar 20, 2011 18:35
Ao invés de simplesmente responder o exercício para você eu vou lhe indicar um lugar onde você pode aprender a fazê-lo sozinho.
Acesse o seguinte canal no YouTube:
http://www.youtube.com/nerckieVocê irá encontrar diversas aulas de Matemática com os conteúdos do Ensino Fundamental e Médio. Inclusive, aulas sobre inequações.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Dan » Dom Mar 20, 2011 18:59
por Dan » Dom Mar 20, 2011 18:59
Se a inequação deve ser maior que zero, então os possíveis valores que o x assume devem ser valores que tornem o resultado da equação maior que zero.
Você precisa analisar os gráficos das equações para chegar a essa conclusão:
Para a primeira equação teremos:

Perceba que para valores entre 1 e 2 o resultado y é negativo. Quando for igual a 1 ou 2 o resultado é zero. Portanto, devem ser considerados apenas os valores menores que 1 ou maiores que 2 para que o resultado da equação seja maior que zero, e portanto positivo.
Para a segunda equação temos:

Ou seja, o resultado y da equação só será positivo para valores entre -1 e 1/2.
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por johnlaw » Dom Mar 20, 2011 19:59
por johnlaw » Dom Mar 20, 2011 19:59
Luiz Aquino, obrigado pela dica, vou verificar os vídeos.
Dan, compreendi, muito obrigado. Mas é possível eu verificar essas condições sem fazer o gráfico ? Somente olhando para a primeira equação por exemplo, como eu concluiria que o conjunto solução está de infinito até 1 (intervalo aberto) e de 2 (intervalo aberto) até infinito ?
Muito Obrigado!
-
johnlaw
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Ago 06, 2010 13:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática Licenciatura
- Andamento: cursando
 por Dan » Dom Mar 20, 2011 20:07
por Dan » Dom Mar 20, 2011 20:07
Só uma correção: formalmente é um intervalo aberto de menos infinito até 1. E aberto em 2 até mais infinito.
Não precisa fazer o gráfico. Basta observa o sinal do

(se for positivo a concavidade da parábola é para cima e se for negativo a concavidade é para baixo). A partir disso você só precisa calcular as raízes e imaginar essa parábola cortando o eixo x nessas raízes. Lembrando que algumas parábolas não cortam o eixo x.
Um esboço sempre facilita essa determinação, mas se você conseguir imaginar sem se confundir, ok.
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Inequação - resultado
por thivalverde » Ter Ago 16, 2011 12:07
- 1 Respostas
- 1568 Exibições
- Última mensagem por Molina

Ter Ago 16, 2011 15:09
Álgebra Elementar
-
- [Inequação] Resultado não confere.
por renanrdaros » Sáb Ago 13, 2011 18:22
- 11 Respostas
- 5375 Exibições
- Última mensagem por renanrdaros

Qua Ago 17, 2011 02:18
Álgebra Elementar
-
- Probabilidade - Dificuldades para compreender e resolver
por LadyTrilleras » Sex Out 11, 2013 16:46
- 2 Respostas
- 2262 Exibições
- Última mensagem por LadyTrilleras

Sex Out 11, 2013 18:00
Probabilidade
-
- [Limite] Limites notáveis -->compreender a propriedade usada
por Nicolas1Lane » Qua Set 25, 2013 20:11
- 2 Respostas
- 1796 Exibições
- Última mensagem por Nicolas1Lane

Qua Set 25, 2013 20:45
Cálculo: Limites, Derivadas e Integrais
-
- resultado diferente - PG
por jose henrique » Qui Set 30, 2010 23:50
- 4 Respostas
- 3206 Exibições
- Última mensagem por MarceloFantini

Ter Out 05, 2010 01:18
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
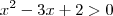 e obtive os dois resultados:
e obtive os dois resultados: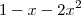 , essa com:
, essa com:

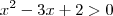 e obtive os dois resultados:
e obtive os dois resultados: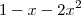 , essa com:
, essa com:






 (se for positivo a concavidade da parábola é para cima e se for negativo a concavidade é para baixo). A partir disso você só precisa calcular as raízes e imaginar essa parábola cortando o eixo x nessas raízes. Lembrando que algumas parábolas não cortam o eixo x.
(se for positivo a concavidade da parábola é para cima e se for negativo a concavidade é para baixo). A partir disso você só precisa calcular as raízes e imaginar essa parábola cortando o eixo x nessas raízes. Lembrando que algumas parábolas não cortam o eixo x.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
