Caeros escreveu:Olá Renato, obrigado por colaborar,mas quem quer saber tem que perguntar:
estou começando a estudar este assunto, então vou lhe perguntar:
1) O que vc está dizendo com "classes de equivalência módulo 8"? sei que congruência é uma relação de equivalência, então vc está dizendo que x = {0, 1, 2, 3, 4, 5, 6, 7} é o conjunto dos restos que se podem ter na divisão por 8 ou os valores que x pode assumir? Quer dizer estes números se relacionam com 8 por ser os retos relacionados a ele na divisão?
Caeros, concordo plenamente, se deseja saber tem mais é que perguntar !!!
Lembre-se que estamos tratando de divisão pelo algoritmo de Euclides, isto é, x = 8k + r, onde r é o resto.. As classes de equivalência na verdade são o que chamamos de partições, elas representam os restos das divisões por 8 (neste caso) então cada classe dessa é um conjunto separado, veja:
Quando falamos de classe 0, por exemplo, estamos falando de todos os números inteiros cuja a divisão por 8 dá resto zero, então 0 = {...,8,16,32,48,..} e quando falamos de classe 1 estamos falando do conjunto dos números inteiros cuja a divisão por 8 dá resto 1, então 1 = {...,9,17,33,49,..}.
Caeros escreveu:2) e o sistema completo de resto módulo 8 para x, então este é o conjunto de números que podem ser restos?
Exatamente, como eu disse anteriormente... Classe 3 significa todos os inteiros cuja a divisão por 8 tenha resto 3, então 3 = {...,11,19,35,51,..}.
Caeros escreveu:3) de onde saiu
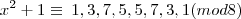
? na resposta que postei pois tirei do material e se estiver errado tenho que corrigir a fonte ou seja onde consegui o material.
Mais uma vez obrigado está me ajudando bastante.

Boa pergunta, eu também quero saber... Se me apresentassem esse problema sem a demonstração, eu teria feito do jeito que escrevi, eu também não entendi a onde o autor obteve esses números e sabe o que é mais interessante ?? Andei pesquisando na internet agora e vi um pdf onde o autor faz o mesmo exercício da mesma maneira, agora eu fiquei confuso, pois devo ter errado em algum lugar (ou no raciocínio da questão)... Vamos esperar o pessoal mais experiente (Luiz Aquino, Molina ou o Fantini) lerem a questão e postarem suas opiniões ou correções.
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
 não tem soluções:
não tem soluções: 0,1,2,3,4,5,6,7(mod8)
0,1,2,3,4,5,6,7(mod8) aqui entendo que é aplicada a propriedade que diz: "Sabemos que a
aqui entendo que é aplicada a propriedade que diz: "Sabemos que a  b(modm)
b(modm)  a = b+mk, para algum k
a = b+mk, para algum k  Z. Neste
Z. Neste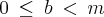 "
"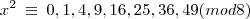
 aqui compreendo que foi aplicada a
aqui compreendo que foi aplicada a 
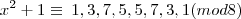
 já aqui não consigo compreender qual propriedade foi aplicada ou como chegou a estes valores????
já aqui não consigo compreender qual propriedade foi aplicada ou como chegou a estes valores???? 



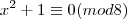
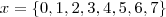
 e usando a propriedade já citada, teremos:
e usando a propriedade já citada, teremos:


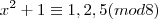

 por 8 é 1.
por 8 é 1.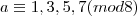
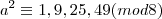
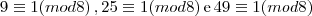 teremos:
teremos: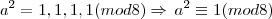

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)