 por Guilherme Carvalho » Qua Mar 16, 2011 16:39
por Guilherme Carvalho » Qua Mar 16, 2011 16:39
Me ajudem nesse por favor
(UFMG) Seja

. O valor da expressão
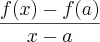
para

, é
a) 0
b) -1
c)
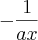
d)
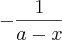
e) a-x
-
Guilherme Carvalho
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Mar 03, 2011 12:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por MarceloFantini » Qua Mar 16, 2011 20:08
por MarceloFantini » Qua Mar 16, 2011 20:08
Qual foi a sua dificuldade? Poste sua tentativa.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Guilherme Carvalho » Sáb Mar 19, 2011 01:13
por Guilherme Carvalho » Sáb Mar 19, 2011 01:13
Então eu tentei eliminar da expressão o f(a), pois ele não esta em nenhuma das respostas... tentei isso colocando o valor de f(x) na expressão mais logo acabei travando.....
-
Guilherme Carvalho
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Mar 03, 2011 12:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por MarceloFantini » Sáb Mar 19, 2011 14:19
por MarceloFantini » Sáb Mar 19, 2011 14:19
Como não tem em nenhuma resposta? Alternativas C, D e E contém o a. Pra ver se está entendendo, calcule pra mim

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Guilherme Carvalho » Seg Mar 21, 2011 11:50
por Guilherme Carvalho » Seg Mar 21, 2011 11:50
agora que percebi a relação aki, vlw pela ajuda cara
f(a)=1/a
-
Guilherme Carvalho
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Mar 03, 2011 12:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por Kelvin Brayan » Ter Mar 22, 2011 00:23
por Kelvin Brayan » Ter Mar 22, 2011 00:23
O maiado eu fiz essa questão, se quiser te ensino !
-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão UFMG
por Guilherme Carvalho » Qui Mar 03, 2011 13:03
- 1 Respostas
- 4771 Exibições
- Última mensagem por Elcioschin

Qui Mar 03, 2011 13:27
Álgebra Elementar
-
- Questão da UFMG
por Kelvin Brayan » Sáb Mar 12, 2011 17:19
- 1 Respostas
- 5005 Exibições
- Última mensagem por Rogerio Murcila

Qua Mar 16, 2011 23:42
Matemática Financeira
-
- Questão da UFMG
por Kelvin Brayan » Dom Mar 13, 2011 16:26
- 4 Respostas
- 2628 Exibições
- Última mensagem por Kelvin Brayan

Seg Mar 14, 2011 00:34
Cálculo: Limites, Derivadas e Integrais
-
- Questão UFMG
por Kelvin Brayan » Dom Mar 27, 2011 13:36
- 2 Respostas
- 4694 Exibições
- Última mensagem por Kelvin Brayan

Dom Mar 27, 2011 14:15
Funções
-
- Questão UFMG
por Kelvin Brayan » Dom Abr 24, 2011 17:18
- 2 Respostas
- 4560 Exibições
- Última mensagem por Kelvin Brayan

Dom Abr 24, 2011 23:05
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 . O valor da expressão
. O valor da expressão 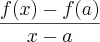 para
para  , é
, é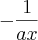
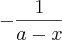

 . O valor da expressão
. O valor da expressão 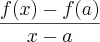 para
para  , é
, é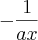
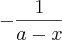



 .
.



