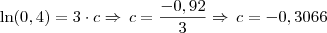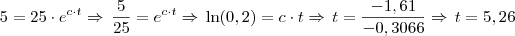por Fabricio dalla » Sex Mar 18, 2011 13:28
por Fabricio dalla » Sex Mar 18, 2011 13:28
Suponha que,ao colocarmos 25kg de açucar na agua,a quantidade de açucar permanece inalterada,apos t horas,seja dada pela função

, com c sendo uma constante real,e A(t) medindo em kg.Se apos tres horas,a quantidade de açucar restante era de 10kg,quanto tempo será necessario para que restem 5kg de açucar?Dados:use as aproximaçoes Ln(0,4)=-0,92 e LN(0,2)=-1,61
até onde fui
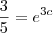
e que
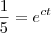
dai elevei ao cubo os 2 menbros da equaçao
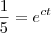
e substitui e fico assim:
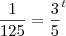
aquele t ali e da fraçao (3/5)
elevado a t
ai morri aqui :(
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Renato_RJ » Sex Mar 18, 2011 14:05
por Renato_RJ » Sex Mar 18, 2011 14:05
Boa tarde Fabrício, tudo em paz ??
Primeiramente precisamos saber o valor da constante c, para isso vamos usar o fato de após 3 horas a quantidade restante de açúcar é de 10 kg, veja:
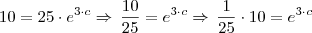
Veja que
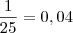
e multiplicado por 10 resulta em 0,4 e então poderemos aplicar o Ln em ambos os lados da igualdade para obtermos o valor de c:
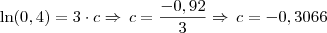
Agora que temos c, podemos obter o tempo necessário para obter os 5 kg.
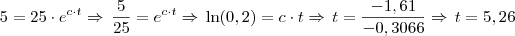
Bem, aí é só converter o 0,26 em minutos para ser mais preciso, o que daria, aproximadamente, 15 minutos, então eu acho que sua resposta seria:
O tempo necessário para obter os 5 kg de açúcar é de 5 horas e 15 minutos.
Espero que eu esteja certo, depois posta a resposta correta...
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Fabricio dalla » Sex Mar 18, 2011 14:22
por Fabricio dalla » Sex Mar 18, 2011 14:22
é isso ai cara e 5h e 15 min. mas pow, a elaboraçao da questão foi muito mal feita prq em 3horas 15kg de açucar foi diluida
na agua entao tinha que usar o 15kg e nao o 10kg mas vlw por tirar minha duvida!!
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função exponencial] Exercício sobre função exponencial
por fff » Ter Jan 07, 2014 17:51
- 3 Respostas
- 4071 Exibições
- Última mensagem por fff

Qua Jan 08, 2014 06:47
Funções
-
- [Exponencial/Logarítmos] exercício ITA
 por fabiomarine » Ter Ago 28, 2012 16:27
por fabiomarine » Ter Ago 28, 2012 16:27
- 5 Respostas
- 3795 Exibições
- Última mensagem por fabiomarine

Qua Ago 29, 2012 13:23
Logaritmos
-
- [Desigualdade] entre função exponencial e função potência
por VitorFN » Sex Mai 26, 2017 15:18
- 1 Respostas
- 5738 Exibições
- Última mensagem por adauto martins

Sex Jul 07, 2017 12:17
Álgebra Elementar
-
- [função exponencial] Exprimir em função de x
por fff » Ter Jan 07, 2014 12:02
- 2 Respostas
- 3125 Exibições
- Última mensagem por fff

Ter Jan 07, 2014 13:23
Funções
-
- funçao exponencial ITA
por zeramalho2004 » Dom Jun 28, 2009 19:55
- 3 Respostas
- 5108 Exibições
- Última mensagem por Marcampucio

Seg Jun 29, 2009 15:23
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , com c sendo uma constante real,e A(t) medindo em kg.Se apos tres horas,a quantidade de açucar restante era de 10kg,quanto tempo será necessario para que restem 5kg de açucar?Dados:use as aproximaçoes Ln(0,4)=-0,92 e LN(0,2)=-1,61
, com c sendo uma constante real,e A(t) medindo em kg.Se apos tres horas,a quantidade de açucar restante era de 10kg,quanto tempo será necessario para que restem 5kg de açucar?Dados:use as aproximaçoes Ln(0,4)=-0,92 e LN(0,2)=-1,61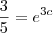
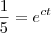
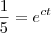
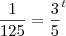


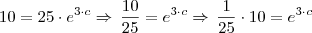
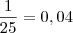 e multiplicado por 10 resulta em 0,4 e então poderemos aplicar o Ln em ambos os lados da igualdade para obtermos o valor de c:
e multiplicado por 10 resulta em 0,4 e então poderemos aplicar o Ln em ambos os lados da igualdade para obtermos o valor de c: