 por Renato_RJ » Qui Mar 17, 2011 23:59
por Renato_RJ » Qui Mar 17, 2011 23:59
Caros colegas, estou resolvendo uns exercícios de um livro de Álgebra da SBM, e existe diversas questões para serem feitas de forma demonstrativa, mas essa eu não tenho tanta certeza se fiz corretamente a demonstração. Alguém poderia verificar e dizer se está correto ?
A questão:
Prove que todo polinômio de grau ímpar sobre

possui uma raiz em

.
A demonstração:
Tenhamos

, como m é ímpar então

é ímpar. Agora tenhamos
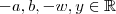
não nulos tais que:
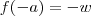
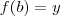
Segundo o Teorema do Valor Intermediário
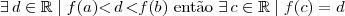
De acordo com o mesmo teorema, se

possuem sinais opostos, então

.
Logo c é a raiz do polinômio em

, então a demonstração está concluída.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por LuizAquino » Sex Mar 18, 2011 10:25
por LuizAquino » Sex Mar 18, 2011 10:25
Eu sugiro que você leia sobre o
Teorema Fundamental da Álgebra:
http://pt.wikipedia.org/wiki/Teorema_fundamental_da_%C3%A1lgebraEm linhas gerais, para demonstrar esse teorema eu tentaria usar o fato que toda raiz complexa aparece aos pares. Isso quer dizer que mesmo que um polinômio de grau ímpar tenha raízes complexas, como elas aparecem aos pares, nós teremos pelo menos uma raiz real.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Renato_RJ » Sex Mar 18, 2011 11:14
por Renato_RJ » Sex Mar 18, 2011 11:14
Luiz, não vou mentir para você, eu até pensei em usar o Teorema Fundamental da Álgebra mas achei que a demonstração ficaria mais complexa e talvez eu não conseguisse concluí-la, por isso pensei em usar o teorema do valor intermediário. Mas vou tentar e posto aqui para discutirmos, o que acha ?
Obrigado pela ajuda,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite do produto] Dúvida na demonstração
por BlackSabbathRules » Sex Mai 09, 2014 16:56
- 3 Respostas
- 3036 Exibições
- Última mensagem por e8group

Sáb Mai 10, 2014 15:23
Cálculo: Limites, Derivadas e Integrais
-
- DEMONSTRAÇÃO
por arima » Seg Nov 08, 2010 08:40
- 8 Respostas
- 5922 Exibições
- Última mensagem por roseli

Qua Nov 10, 2010 21:03
Álgebra Elementar
-
- Demonstração
por Lorettto » Qui Dez 16, 2010 23:03
- 3 Respostas
- 2268 Exibições
- Última mensagem por Elcioschin

Seg Dez 20, 2010 12:39
Álgebra Elementar
-
- Demonstração
por Pedro2 » Sáb Mar 12, 2011 15:38
- 1 Respostas
- 1956 Exibições
- Última mensagem por Guill

Sex Abr 20, 2012 16:01
Matrizes e Determinantes
-
- PA - Demonstração
por jessicaccs » Sex Mar 25, 2011 11:52
- 1 Respostas
- 1468 Exibições
- Última mensagem por Elcioschin

Sex Mar 25, 2011 14:55
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 possui uma raiz em
possui uma raiz em  .
. , como m é ímpar então
, como m é ímpar então é ímpar. Agora tenhamos
é ímpar. Agora tenhamos 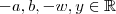 não nulos tais que:
não nulos tais que: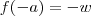
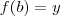
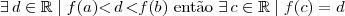
 possuem sinais opostos, então
possuem sinais opostos, então  .
. , então a demonstração está concluída.
, então a demonstração está concluída.







