 por Cleyson007 » Qui Mar 17, 2011 23:50
por Cleyson007 » Qui Mar 17, 2011 23:50
Boa noite a todos!
Bom, estou começando a disciplina de Cálculo II, e estou tendo dificuldade nesse início com as integrais.
Bom, vamos a um exercício bem simples até que eu vá aprendendo os "macetes":
Prove que

A apostila que uso descreve o seguinte:
"Sabendo que F(x) é uma primitiva de f(x), temos que

". Primeiramente, explique-me essa notação. Depois explique o procedimento de resolução passo-a-passo.
Aguardo retorno.
Agradeço a atenção.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por OsmarFraga » Sex Mar 18, 2011 03:08
por OsmarFraga » Sex Mar 18, 2011 03:08
Bom, essa notação é definição de integral definida.

Então, calcula-se a integral de

que seria:
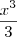
Segundo a definição de integral definida, tem-se:

c.q.d.
-
OsmarFraga
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Nov 16, 2010 15:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciature Plena Em Matemática
- Andamento: cursando
 por MarceloFantini » Sex Mar 18, 2011 05:56
por MarceloFantini » Sex Mar 18, 2011 05:56
Inverteu a ordem na subtração, estaria errado.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Sex Mar 18, 2011 10:29
por LuizAquino » Sex Mar 18, 2011 10:29
Prezado Cleyson007,
Recomendo que veja o tópico:
Livros On-lineviewtopic.php?f=137&t=4087Vale a pena ler um pouco sobre o assunto antes de postar as dúvidas.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema - Estudando P/ Concurso
por m3oliveira » Qua Abr 13, 2011 10:24
- 1 Respostas
- 1304 Exibições
- Última mensagem por Abelardo

Qua Abr 13, 2011 14:15
Números Complexos
-
- Estudando Inequações Dúvida
por LuizCarlos » Ter Abr 03, 2012 23:54
- 3 Respostas
- 1989 Exibições
- Última mensagem por MarceloFantini

Qua Abr 04, 2012 19:18
Inequações
-
- limites.. estou estudando limites e
por jeffinps » Ter Mar 12, 2013 12:31
- 1 Respostas
- 1005 Exibições
- Última mensagem por Douglas16

Ter Mar 12, 2013 14:29
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4611 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4575 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 ". Primeiramente, explique-me essa notação. Depois explique o procedimento de resolução passo-a-passo.
". Primeiramente, explique-me essa notação. Depois explique o procedimento de resolução passo-a-passo.



 que seria:
que seria: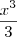





 .
.



