 por 380625 » Qui Mar 17, 2011 11:21
por 380625 » Qui Mar 17, 2011 11:21
Bom dia gostaria que me ajudasem a provar:
|x-y|>|x|-|y|, o sinal é de maior igual.
Consegui provar elevando os dois lados ao quadrado porem, meu professor me disse que faltou justificar certas propriedades e passagens, queria saber se alguem poderia provar e me mostrar as passagens.
Grato.
Flávio Santana.
-
380625
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Sex Fev 18, 2011 17:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por LuizAquino » Qui Mar 17, 2011 11:33
por LuizAquino » Qui Mar 17, 2011 11:33
Poste aqui todas as passagens que você fez. Desse modo, podemos identificar os problemas.
De qualquer modo, há uma estratégia algébrica para realizar a demonstração.
Considere que já tenha sido provada a Desigualdade Triangular:

.
Vejamos agora como demonstrar a desigualdade

.
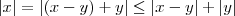
Ou seja, temos que:


Portanto, temos que:
 Observação
ObservaçãoDemonstração da Desigualdade Triangular.
Segue da definição de módulo, que para quaisquer números reais
a e
b temos que:
(i)

(ii)
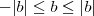
Somando-se os membro dessas inequações:

Segue da definição de módulo, que se

, com
c > 0, então temos que

. Sendo assim, fazendo
x = a + b e
c = |a| + |b|, temos que:

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por LuizAquino » Sex Set 09, 2011 10:47
por LuizAquino » Sex Set 09, 2011 10:47
Correção
Onde há
"Somando-se os membro dessas inequações (...)"
leia-se
"Somando-se os membros dessas inequações (...)"
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Módulo
por Rodrigo Tomaz » Sex Fev 19, 2010 11:36
- 4 Respostas
- 3009 Exibições
- Última mensagem por MarceloFantini

Sex Mar 05, 2010 16:09
Funções
-
- Modulo
por Sandy26 » Ter Abr 27, 2010 14:46
- 5 Respostas
- 2998 Exibições
- Última mensagem por MarceloFantini

Qui Abr 29, 2010 17:57
Álgebra Elementar
-
- Módulo
por Bebel » Dom Ago 08, 2010 00:24
- 0 Respostas
- 1377 Exibições
- Última mensagem por Bebel

Dom Ago 08, 2010 00:24
Números Complexos
-
- Módulo
por torilleon » Sáb Ago 20, 2011 19:28
- 2 Respostas
- 1579 Exibições
- Última mensagem por Neperiano

Sáb Ago 20, 2011 20:40
Álgebra Elementar
-
- modulo
por rodrigonapoleao » Seg Jan 21, 2013 13:19
- 1 Respostas
- 1504 Exibições
- Última mensagem por e8group

Seg Jan 21, 2013 15:23
Inequações
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 .
. .
.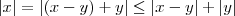




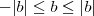

 , com
, com  . Sendo assim, fazendo
. Sendo assim, fazendo 



 , avisa que eu resolvo.
, avisa que eu resolvo.

