 (Primeira Imagem). A fórmula para a união de dois conjuntos é algo quase intuitivo, logo decompus eles nas respectivas formas simples -->
(Primeira Imagem). A fórmula para a união de dois conjuntos é algo quase intuitivo, logo decompus eles nas respectivas formas simples -->  . Somando tudo terei que
. Somando tudo terei que 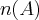 ,
, 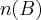 e
e 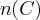 estão repetidos, assim tomei só um de cada, ficando com
estão repetidos, assim tomei só um de cada, ficando com  =
=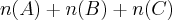 ; tenho elementos que podem pertencer a mais de um conjunto, logo retirei todas as intercecções, ficando com
; tenho elementos que podem pertencer a mais de um conjunto, logo retirei todas as intercecções, ficando com  =
= .
.A dúvida que tenho é que já vi a fórmula e não entendi o porque do
 no final dela. Essa adição dos elementos em comum dos três conjuntos é devida as respectivas subtrações das intersecções que fiz? Qual seria a explicação... caso haja uma demonstração (e sei que tem), por favor, expliquem. Qualquer coisa, esse é meu email ---> abelardo_92_92@hotmail.com
no final dela. Essa adição dos elementos em comum dos três conjuntos é devida as respectivas subtrações das intersecções que fiz? Qual seria a explicação... caso haja uma demonstração (e sei que tem), por favor, expliquem. Qualquer coisa, esse é meu email ---> abelardo_92_92@hotmail.com

 .
.
 . Sendo assim, ficamos com:
. Sendo assim, ficamos com:
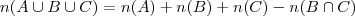
![- [n(A \cap B) + n(A \cap C) - n(A \cap B \cap C)] - [n(A \cap B) + n(A \cap C) - n(A \cap B \cap C)]](/latexrender/pictures/dacef931d477d4eae8324bf8a03340bf.png)

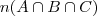 no final da fórmula. Note que quando fazemos a soma
no final da fórmula. Note que quando fazemos a soma 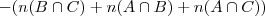 . Desse modo, até aqui aquele termo não havia sido contado. Por isso que ao final devemos adicioná-lo.
. Desse modo, até aqui aquele termo não havia sido contado. Por isso que ao final devemos adicioná-lo.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.