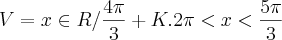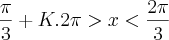por Cleyson007 » Qua Set 24, 2008 19:44
por Cleyson007 » Qua Set 24, 2008 19:44
Olá Fábio, tudo bem? Estou com uma dúvida e gostaria mais uma vez de sua ajuda.
A questão é a seguinte:
Resolva as equações trigonométricas determinando inicialmente a solução para
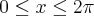
.
a) sen x >
![\frac{- \sqrt[]{3}}{2} \frac{- \sqrt[]{3}}{2}](/latexrender/pictures/9d638a5ced0682ea6e81a7cd8f815ef5.png)
b) sen x <
![\frac{\sqrt[]{3}}{2} \frac{\sqrt[]{3}}{2}](/latexrender/pictures/21682d7c1e802e9b52a99c01850489c4.png)
Eu resolvi a letra "A" da seguinte maneira: sen x >
![-\frac{\sqrt[]{3}}{2} -\frac{\sqrt[]{3}}{2}](/latexrender/pictures/3eccd1109c9de4901a3f78a67e9673fe.png)
= sen x >


e
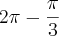
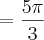
. Daí o conjunto verdade é:
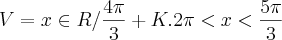
Na letra "B" eu resolvi bem assim: sen x <


O conjunto verdade é: V= {
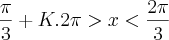
Está correta a minha resolução? Ajude-me por favor. Muito obrigado!
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Sandra Piedade » Ter Set 30, 2008 08:19
por Sandra Piedade » Ter Set 30, 2008 08:19
Olá Cleyson007!
Não sou o Fábio, e acabei mesmo agora de me registar; como entretanto já vi que qualquer um pode ajudar, mas sem resolver o exercício, e como eu gosto muito de ajudar, vou tentar, se depois o Fábio entender que o deve fazer, responderá a seguir, penso eu.
Vi a sua resolução da letra A e, se não me engano, há um pequeno erro que faz com que o conjunto verdade esteja ao contrário... Ora tente substituir um elemento do seu conjunto e ver se verifica a inequação (essa é uma forma prática de ver se um exercício deste tipo poderá estar correcto ou não, embora não seja suficiente). Depois de experimentar, diga o que concluiu e tente descobrir o seu erro. Não sei se no Brasil se aprende a ver o círculo trigonométrico, mas se souber, tente usa-lo para descobrir o seu erro.
Na resolução da letra B o raciocínio é idêntico. Diga depois como ficou, ok? Bom estudo!
-

Sandra Piedade
- Colaborador - em formação

-
- Mensagens: 40
- Registrado em: Ter Set 30, 2008 07:25
- Localização: Setúbal, Portugal
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic em Ensino da Matemática (Portugal)
- Andamento: cursando
-
 por admin » Ter Set 30, 2008 19:08
por admin » Ter Set 30, 2008 19:08
Olá Cleyson!
Olá Sandra, boas-vindas e obrigado por ajudar!
Cleyson, siga a dica com o apoio do círculo trigonométrico para raciocinar sobre a coerência dos intervalos obtidos.
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [trigonometria] trigonometria em triangulo qualquer
por biamassa00 » Sex Mai 25, 2012 22:19
- 0 Respostas
- 3588 Exibições
- Última mensagem por biamassa00

Sex Mai 25, 2012 22:19
Trigonometria
-
- (Trigonometria) problema trigonometria
por Luizap11 » Qui Dez 05, 2013 00:33
- 2 Respostas
- 5258 Exibições
- Última mensagem por Edunclec

Qui Dez 05, 2013 20:53
Trigonometria
-
- trigonometria
por Micheline » Dom Jan 25, 2009 16:21
- 5 Respostas
- 4946 Exibições
- Última mensagem por Cleyson007

Seg Jan 26, 2009 17:27
Trigonometria
-
- Trigonometria
por Flavio » Sex Fev 13, 2009 21:29
- 5 Respostas
- 5102 Exibições
- Última mensagem por Molina

Seg Fev 16, 2009 01:53
Trigonometria
-
- Trigonometria
 por rybb » Ter Ago 25, 2009 00:48
por rybb » Ter Ago 25, 2009 00:48
- 1 Respostas
- 2495 Exibições
- Última mensagem por Lucio Carvalho

Ter Ago 25, 2009 06:57
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
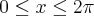 .
.![\frac{- \sqrt[]{3}}{2} \frac{- \sqrt[]{3}}{2}](/latexrender/pictures/9d638a5ced0682ea6e81a7cd8f815ef5.png)
![\frac{\sqrt[]{3}}{2} \frac{\sqrt[]{3}}{2}](/latexrender/pictures/21682d7c1e802e9b52a99c01850489c4.png)
![-\frac{\sqrt[]{3}}{2} -\frac{\sqrt[]{3}}{2}](/latexrender/pictures/3eccd1109c9de4901a3f78a67e9673fe.png) = sen x >
= sen x > 
 e
e 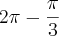
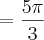 . Daí o conjunto verdade é:
. Daí o conjunto verdade é: