Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por LuizAquino » Qua Fev 23, 2011 22:15
por LuizAquino » Qua Fev 23, 2011 22:15
Eis um exercício curioso onde podemos aplicar os conceitos de P.A..
Seja a sequência formada por cada número inteiro positivo n repetido n vezes, em ordem crescente. Isto é, seja a sequência {1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, ...}. Determine a soma entre os termos na posição 4.460 e 4.470 dessa sequência. (Resposta: 189).
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Renato_RJ » Sex Mar 11, 2011 07:57
por Renato_RJ » Sex Mar 11, 2011 07:57
Luiz, essa sequência é o mesmo que

????
Se sim, então estou indo pelo caminho certo ? Pois desse jeito eu chego na PA mas não consigo chegar na soma, o valor que eu acho é muito maior do que o do gabarito.. Vou pensar um pouco mais...
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por LuizAquino » Sex Mar 11, 2011 10:48
por LuizAquino » Sex Mar 11, 2011 10:48
Renato_RJ escreveu:Luiz, essa sequência é o mesmo que

?
Não. Perceba que o que você colocou aqui é uma
soma, não uma
sequência. Ainda que você escrevesse
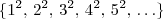
não seria a mesma sequência.
DicaA quantidade de vezes que cada número é repetido na sequência forma uma P.A.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Abelardo » Sex Mar 11, 2011 13:03
por Abelardo » Sex Mar 11, 2011 13:03
Tentei também, mas deu um número estratosférico. Quero ver como é que se resolve, tinha uma questão parecida em uma prova da OBM.. era a soma também de números que ocupavam deternimadas posições, números gigantescos e a resposta era nove! (Se não me falhe a memória) kkk
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Renato_RJ » Sex Mar 11, 2011 15:07
por Renato_RJ » Sex Mar 11, 2011 15:07
LuizAquino escreveu:Renato_RJ escreveu:Luiz, essa sequência é o mesmo que

?
Não. Perceba que o que você colocou aqui é uma
soma, não uma
sequência. Ainda que você escrevesse
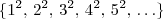
não seria a mesma sequência.
DicaA quantidade de vezes que cada número é repetido na sequência forma uma P.A.
Então teremos uma PA desse jeito ?

Pois o elemento 1 só parece uma vez (e é o primeiro elemento da PA), enquanto que o elemento 2 aparece duas vezes, o 3 aparece 3 vezes e assim sucessivamente.. Então o elemento 20, por exemplo, aparecerá 20 vezes ?
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por LuizAquino » Sex Mar 11, 2011 15:10
por LuizAquino » Sex Mar 11, 2011 15:10
Renato_RJ escreveu:Então teremos uma PA desse jeito ?
P.A. = {1, 2, 3, 4, 5, ... }
Sim. A quantidade de vezes que cada número é repetido forma uma P.A. de primeiro termo 1 e razão também 1.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Renato_RJ » Sex Mar 11, 2011 15:16
por Renato_RJ » Sex Mar 11, 2011 15:16
LuizAquino escreveu:Renato_RJ escreveu:Então teremos uma PA desse jeito ?
P.A. = {1, 2, 3, 4, 5, ... }
Sim. A quantidade de vezes que cada número é repetido forma uma P.A. de primeiro termo 1 e razão também 1.
Então estou caindo na pegadinha...
O elemento que está na posição 4460 é o próprio, por exemplo ??
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por LuizAquino » Sex Mar 11, 2011 15:27
por LuizAquino » Sex Mar 11, 2011 15:27
Renato_RJ escreveu:O elemento que está na posição 4460 é o próprio, por exemplo ??
Não. O numero que está na posição 4460 da sequência não é o número 4460.
Por exemplo, note que o primeiro número 5 aparece na posição 11 da sequência.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Renato_RJ » Sáb Mar 12, 2011 03:06
por Renato_RJ » Sáb Mar 12, 2011 03:06
Mestre acho que matei a charada, veja...
Chamei de n o número da sequência e acabei percebendo que quando temos n =1 teremos 1 termo, mas quando temos n = 2 teremos 3 termos, n = 3 teremos 6 termos e assim por diante (n = 4 serão 10 termos, n = 5 serão 15 termos, etc), logo quando n for igual a k teremos a soma de todos os termos até k então basta igualar a soma da PA ao termo desejado veja:

Fazendo o mesmo para o termo 4470:
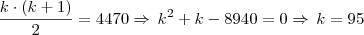
Tive que arredondar os valores pois tinha me esquecido que se tratava de uma sequência de números inteiros, então a soma dos dois será 189.
Acertei ???
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por LuizAquino » Sáb Mar 12, 2011 09:10
por LuizAquino » Sáb Mar 12, 2011 09:10
É isso mesmo.
Apenas para deixar claro, teremos que:
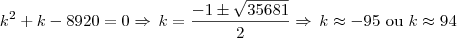

Devemos descartar os valores negativos.
Teremos que o número 94 aparecerá nas posições de 4372 até 4465. Já o número 95 aparecerá nas posições de 4466 até 4560.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Molina » Sáb Mar 12, 2011 13:53
por Molina » Sáb Mar 12, 2011 13:53
Bom dia, Luiz e Renato.
Quando estava tentando este desafio, pra começar li errada a questão. Li que deveríamos descobri a soma da posição 4.460
a 4.470 e não
e como é o enunciado correto. Mas fiz por este caminho que é a solução e chegando ao mesmo valor quebrado que vocês chegaram, mas como se tratava de números interos, então achei que estava errado.
Mas bom ver a solução e ve que eu estava próximo de descobrir.
Valeu,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Desafios Médios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [sequencia] Calcular limite de sequencia por definição
 por amigao » Ter Abr 15, 2014 15:15
por amigao » Ter Abr 15, 2014 15:15
- 4 Respostas
- 3997 Exibições
- Última mensagem por e8group

Dom Mai 11, 2014 17:09
Sequências
-
- Expressão numérica
por thadeu » Qua Nov 18, 2009 16:12
- 1 Respostas
- 2683 Exibições
- Última mensagem por Elcioschin

Qua Nov 18, 2009 18:44
Álgebra Elementar
-
- Expressão numerica
por karenblond » Ter Mai 15, 2012 23:55
- 6 Respostas
- 4006 Exibições
- Última mensagem por Cleyson007

Ter Mai 22, 2012 19:50
Funções
-
- [Expressao Numerica]
 por lokido_ » Dom Out 11, 2015 03:34
por lokido_ » Dom Out 11, 2015 03:34
- 4 Respostas
- 2816 Exibições
- Última mensagem por adauto martins

Qui Out 15, 2015 19:14
Funções
-
- Dificuldade na expressã numérica
por mazoni » Seg Jun 21, 2010 18:09
- 1 Respostas
- 1220 Exibições
- Última mensagem por gustavowelp

Seg Jun 28, 2010 19:10
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 ????
????
 ?
?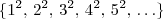 não seria a mesma sequência.
não seria a mesma sequência.

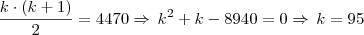
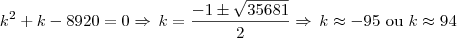



 .
.



