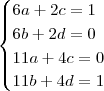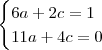por oliveiracld » Qua Mar 09, 2011 00:38
por oliveiracld » Qua Mar 09, 2011 00:38
tenho dificuldade em matematica por issovenho lhes pedir ajuda. quero tentar reslver a seguinte matriz
- Código: Selecionar todos
6 2 a b 1 0
=
11 4 c d 0 1
6a + 2c=1 6b +2d = 0 11a +4c = 0 11b + 4d = 1
nao sei por onde começara a resolver se tivese por exemplo a+ 5c =1 eu saberia começar mais assim eu nao estou me perco
-
oliveiracld
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Mar 09, 2011 00:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: lic. computação
- Andamento: cursando
 por LuizAquino » Qua Mar 09, 2011 11:00
por LuizAquino » Qua Mar 09, 2011 11:00
O que você tem é o exercício: Determinar a, b, c e d tais que

Multiplicando-se as duas matrizes do primeiro membro e comparando os elementos com a matriz do segundo membro, obtemos o sistema de equações:
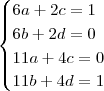
Nós podemos separar esse sistema em dois:
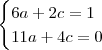

Agora, é só resolver cada um desses sistemas.
Aproveito para lhe sugerir que dê uma olhada no tópico:
Aulas de Matemática no YouTubeviewtopic.php?f=120&t=3818
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por oliveiracld » Qua Mar 09, 2011 17:50
por oliveiracld » Qua Mar 09, 2011 17:50
valeu obrigado vou tntar resolver e posto resultado final. se conseguir hehe
-
oliveiracld
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Mar 09, 2011 00:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: lic. computação
- Andamento: cursando
 por oliveiracld » Qua Mar 09, 2011 18:44
por oliveiracld » Qua Mar 09, 2011 18:44
- Código: Selecionar todos
{6a + 2c = 1 ( - 2) // multipliquei por -2 6b +2d =0 (- 2) <-
11a+ 4c = 0 <- 11b + 4d =1
{ -12a - 4c = -2 {-12b - 4d =0
11a + 4c = 0 11b +4d = 1
- a = -2 (-1) - b = 1 ( - 1)
b = - 1
a = 2 6b + 2d =0
11 * a +4c =0 6 * ( - 1) +2d =0
22 +4c =0 - 6 + 2d =0
4c = - 22 2d = 6
c = -22 / 4 d = 6/2
d = 3
a = 2, b = - 1, c = - 22/4 ? d = 3
nao entendi pq fica 11/2, se eu tneho que pegar 11 x o valor de A que e 2, depois continua 4c ai na linha debaixo continua ate eu passar o o C = - 22 / 4 nao e assim a outra arrumei mais essa aqui eu enrosquei nao consegui entender
resolvi mais porque so na letra C que nao da resolução ? fica 22/4 se dividir da numers quebrados, e asism que faz o exxercicio ? sei que e dessa maneira que faz mais esta errado onde errei ?
:?
naoconseui inserir formulas nao naoachei a chaves
Editado pela última vez por
oliveiracld em Qui Mar 10, 2011 14:39, em um total de 2 vezes.
-
oliveiracld
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Mar 09, 2011 00:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: lic. computação
- Andamento: cursando
 por LuizAquino » Qua Mar 09, 2011 20:19
por LuizAquino » Qua Mar 09, 2011 20:19
oliveiracld escreveu:resolvi mais porque so na letra C que nao da resolução ? fica 22/4 se dividir da numers quebrados, e asism que faz o exxercicio ? sei que e dessa maneira que faz mais esta errado onde errei ?
Não há problema algum no resultado do exercício haver números não inteiros. Aliás, acostume-se logo com
todos os números reais (naturais, inteiros, racionais e irracionais).
Além disso, revise suas contas, pois a resposta correta é:
a=2,
b=-1,
c=-11/2 e
d=3. Note que você errou o sinal da maioria das soluções.
Agora, uma dica:
Ao editar suas mensagens use o botão "Editor de Fórmulas". Com ele você poderá colocar todos os símbolos e notações matemáticas adequadas usando o sistema LaTeX. Leia mais sobre isso no tópico:
DICA: Escrevendo Fórmulas com LaTeX via BBCodeviewtopic.php?f=9&t=74
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- DIFICULDADE EM RESOLVER MATRIZ INVERSA AJUDA POR FAVOR.
por werkander » Qui Mar 17, 2011 15:50
- 2 Respostas
- 2485 Exibições
- Última mensagem por werkander

Qui Mar 17, 2011 20:01
Matrizes e Determinantes
-
- Dificuldade em resolver o exercicio nº 2
por Catriane Moreira » Sáb Nov 20, 2010 23:01
- 1 Respostas
- 2170 Exibições
- Última mensagem por alexandre32100

Seg Nov 22, 2010 14:42
Matemática Financeira
-
- Dificuldade ao resolver uma Integral Racinal
por rubenesantos » Seg Mai 02, 2011 22:38
- 1 Respostas
- 1826 Exibições
- Última mensagem por LuizAquino

Seg Mai 02, 2011 22:58
Cálculo: Limites, Derivadas e Integrais
-
- [Funções] dificuldade para resolver
por tiaguito » Seg Out 22, 2012 17:01
- 1 Respostas
- 1834 Exibições
- Última mensagem por Russman

Seg Out 22, 2012 18:35
Funções
-
- Matriz Inversa
por Cleyson007 » Qui Ago 20, 2009 17:49
- 5 Respostas
- 4482 Exibições
- Última mensagem por Cleyson007

Sáb Ago 22, 2009 10:45
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.