 .
. Estou estudando sobre números primos e há um tópico especial falando sobre os ''números de Mersenne''. Como o a base é 2, o seu resultado é par, mas tem a subtração que o torna um número impar..
pensei em fatorá-lo, mas não vi como. Pensei em um produto notável, mas não tem ''futuro prático'', ficaria inúmeros fatores.


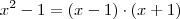
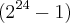 ?
?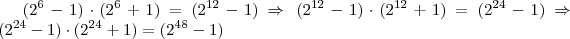

 sabemos que os dois divisores que se encontram no intervalo dado só podem ser
sabemos que os dois divisores que se encontram no intervalo dado só podem ser  e
e  .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)