 por Abelardo » Seg Mar 07, 2011 05:01
por Abelardo » Seg Mar 07, 2011 05:01
Mostre que, se

são racionais e

, então existe um racional r tal que
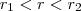
!!
Devo utilizar indução matemática? Caso sim, estou ferrado, como estou no ensino médio, ainda estou pegando o jeito dessa ferramento super poderosa.
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Renato_RJ » Seg Mar 07, 2011 06:14
por Renato_RJ » Seg Mar 07, 2011 06:14
Caro Abelardo, bem vindo ao forum !!!
Deixe-me lembrá-lo que a prova por indução só é efetiva para o conjunto dos números Naturais, neste caso basta você provar que entre dois números racionais sempre existirá outro, racional ou não (no caso dos irracionais).... Talvez a demonstração de Cantor para a infinidade dos Irracionais (entre cada número racional existe uma infinidade de irracionais) lhe ajude.
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Abelardo » Seg Mar 07, 2011 06:38
por Abelardo » Seg Mar 07, 2011 06:38
Obrigado cara, desculpa a minha santa ignorância, ótimo saber disso.. pego só arquivos na net sobre indução, não conheço nenhum livro que fale disso. Dizem que é ferramenta valiosa para olimpíadas de matemática. Sobre a pergunta, não conheço a demonstração. Vou procurá-la!
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Seg Mar 07, 2011 13:21
por MarceloFantini » Seg Mar 07, 2011 13:21
Simples: tome
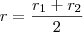
. Obrigatoriamente,

e

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Abelardo » Seg Mar 07, 2011 13:38
por Abelardo » Seg Mar 07, 2011 13:38
Super simples mesmo.. obrigado!
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Conjuntos numéricos
por Marcampucio » Ter Set 01, 2009 21:50
- 1 Respostas
- 1444 Exibições
- Última mensagem por Elcioschin

Ter Set 01, 2009 22:38
Álgebra Elementar
-
- Conjuntos numericos
por cristina » Seg Set 14, 2009 18:41
- 1 Respostas
- 1629 Exibições
- Última mensagem por Molina

Ter Set 15, 2009 16:07
Álgebra Elementar
-
- CONJUNTOS NUMÉRICOS
por shallon » Qua Out 28, 2009 23:38
- 0 Respostas
- 1217 Exibições
- Última mensagem por shallon

Qua Out 28, 2009 23:38
Álgebra Elementar
-
- CONJUNTOS NUMÉRICOS
por shallon » Qua Out 28, 2009 23:40
- 0 Respostas
- 1252 Exibições
- Última mensagem por shallon

Qua Out 28, 2009 23:40
Álgebra Elementar
-
- CONJUNTOS NUMÉRICOS
por shallon » Qua Out 28, 2009 23:42
- 0 Respostas
- 1052 Exibições
- Última mensagem por shallon

Qua Out 28, 2009 23:42
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 são racionais e
são racionais e  , então existe um racional r tal que
, então existe um racional r tal que 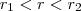 !!
!!
 são racionais e
são racionais e  , então existe um racional r tal que
, então existe um racional r tal que 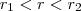 !!
!!



