 por Abelardo » Seg Mar 07, 2011 00:36
por Abelardo » Seg Mar 07, 2011 00:36
(PUC - RJ) Para a, b e c distintos, o valor da expressão
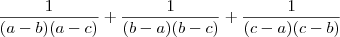
é:
a) a + b + c
b) sempre zero
c) a.b.c
d) 3(a + b + c)
e)
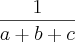
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Renato_RJ » Seg Mar 07, 2011 16:18
por Renato_RJ » Seg Mar 07, 2011 16:18
Abelardo, eu fiz o mmc e depois simplifiquei a expressão e cheguei no seguinte :

Essa expressão resulta em zero, por isso eu acho que a resposta seja a letra b..
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Abelardo » Seg Mar 07, 2011 18:34
por Abelardo » Seg Mar 07, 2011 18:34
vc considerou que (a - b) é igual a (b - a)? não consegui simplificá-lo..
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Renato_RJ » Seg Mar 07, 2011 19:00
por Renato_RJ » Seg Mar 07, 2011 19:00
Abelardo escreveu:vc considerou que (a - b) é igual a (b - a)? não consegui simplificá-lo..
Não os considerei iguais, apenas tive um trabalho gigantesco em desenvolver todo o polinômio e cancelar os termos simétricos, depois simplifiquei o que sobrou...
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Abelardo » Ter Mar 08, 2011 12:02
por Abelardo » Ter Mar 08, 2011 12:02
Que técnica legal essa, nunca pensei em multiplicar por -1! Mais uma técnica. Obrigado Aquino
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Abelardo » Dom Mai 08, 2011 16:37
por Abelardo » Dom Mai 08, 2011 16:37
Desculpe-me profº Luiz Aquino por revirar uma questão antiga, mas fiquei com uma dúvida (Em outro fórum um amigo postou a mesma questão e apresentei a sua resolução e dei todos os créditos ao senhor, é óbvio).
Poderíamos dar valores para ''a'',''b'' e ''c'' ? Se sim, poderiam ser, respectivamente, 5, 4 e 3?
Não sei se posso fazer essa ''substituição'', mas substituindo mesmo assim encontrei valores diferentes -->
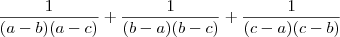
(encontrei zero)

(encontrei - 1)
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Dom Mai 08, 2011 17:29
por LuizAquino » Dom Mai 08, 2011 17:29
Você pode substituir a, b e c por qualquer valor real, desde que eles sejam todos distintos.
Para a=5, b=4 e c=3 temos:
(i)


(ii)


Em ambos os casos, como era de se esperar, o valor final é 0.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Aritmética- Duvida em questão do livro praticando aritmética
por wellkirby » Sex Ago 28, 2015 17:37
- 1 Respostas
- 3493 Exibições
- Última mensagem por wellkirby

Seg Set 07, 2015 23:15
Aritmética
-
- Álgebra Elementar
por Abelardo » Seg Mar 14, 2011 18:09
- 1 Respostas
- 2313 Exibições
- Última mensagem por LuizAquino

Seg Mar 14, 2011 18:21
Álgebra Elementar
-
- Problema Elementar de Sin, Cos e Tan
por ronneysantos » Qui Mar 31, 2011 11:31
- 3 Respostas
- 2903 Exibições
- Última mensagem por ronneysantos

Qui Mar 31, 2011 14:08
Trigonometria
-
- Álgebra Elementar
por Thiago Josep » Sex Set 05, 2014 15:32
- 1 Respostas
- 2666 Exibições
- Última mensagem por DanielFerreira

Qui Jan 01, 2015 22:22
Álgebra Elementar
-
- Exercicio-Algebra elementar
por Renks » Seg Fev 14, 2011 20:38
- 3 Respostas
- 4731 Exibições
- Última mensagem por Renks

Ter Fev 15, 2011 13:55
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
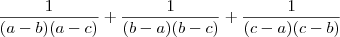 é:
é: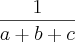

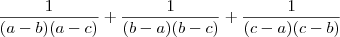 é:
é: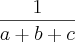





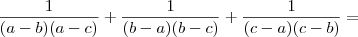
![= \frac{1}{(a-b)(a-c)} + \frac{1}{[(-1)(a-b)][(-1)(c-b)]} +\frac{1}{[(-1)(a-c)](c-b)} = \frac{1}{(a-b)(a-c)} + \frac{1}{[(-1)(a-b)][(-1)(c-b)]} +\frac{1}{[(-1)(a-c)](c-b)}](/latexrender/pictures/058cca2cdd8c50d9460e7d0d0ea8b176.png)




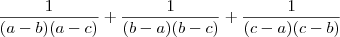 (encontrei zero)
(encontrei zero)  (encontrei - 1)
(encontrei - 1)





 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
