Fabricio dalla escreveu:AEW!! ACERTEI O/
LuizAquino eu fiz de um jeito diferente vê se ta certo!?!
desenhei os 3 diagramas e dei um valor pras interseçoes,e dei o valor de x para o numero de alunos que acertaram as 3 questoes
(y-x)+(w-x)+(z-x)+(x)=52 pois ele fala q 52 alunos acertaram no minimo 2 questoes, logo inclui-se quem acertou
3 questoes.dai fiz o seguinte 80-52=28-8 alunos q erram todas as questoes tenho 20 alunos q acertaram somente uma questao das 3
dai fiz:
[56-(y-x+x+w-x)]+[48-(y-x+x+z-x)]+[32-(w-x+x+z-x)]=20 equaçao I : y+w-2x+z=52
[56-(y+w-x)]+[48-(y+z-x)]+[32-(w+z-x)]=20 [y+w+z]=52+2x X(2)
-2y-2w-2z+3x+136=20 : : 2y+2w+2z=104+4x
-2y-2w-2z+3x=-116 X(-1)
2y+2w+2z-3x=116 equaçao II
substituindo equa I na II temos
104+4x-3x=116 logo tem-se x=12
Tenha cuidado como você escreve a sua solução! Se você for fazer uma prova que tenha questões discursivas, provavelmente você perderia pontos (se não a questão inteira) por causa dessa
bagunça!
Primeiro, temos que

. Você deveria ter organizado com algo como: 80 - 52 = 28 pessoas fizeram apenas 1 questão ou nenhuma delas. Desse modo, 28-8=20 pessoas fizeram apenas 1 questão.
Agora, temos a equação:
(i) y+w-2x+z=52, que é equivalente a 2y+2w+2z=104+4x.
Em seguida, temos a equação:
(ii) [56-(y-x+x+w-x)]+[48-(y-x+x+z-x)]+[32-(w-x+x+z-x)]=20, que é equivalente a equação 2y+2w+2z-3x=116.
Substituindo (i) em (ii), nós obtemos que 104+4x-3x=116, de onde calculamos que x=12.
Por fim, se você analisar direitinho as suas equações verá que a sua solução e a minha são semelhantes. A diferença básica é que eu usei a notação para número de elementos de um conjunto, enquanto que você não usou.



 .
.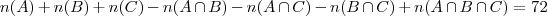
![56 + 48 + 32 - [52 + 2n(A\cap B\cap C)] + n(A\cap B\cap C) = 72 56 + 48 + 32 - [52 + 2n(A\cap B\cap C)] + n(A\cap B\cap C) = 72](/latexrender/pictures/95bfce476288b03e9d3b3ef74e52820e.png)


 . Você deveria ter organizado com algo como: 80 - 52 = 28 pessoas fizeram apenas 1 questão ou nenhuma delas. Desse modo, 28-8=20 pessoas fizeram apenas 1 questão.
. Você deveria ter organizado com algo como: 80 - 52 = 28 pessoas fizeram apenas 1 questão ou nenhuma delas. Desse modo, 28-8=20 pessoas fizeram apenas 1 questão.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)