Estou fazendo Cálculo I e estou tendo dificuldade no conceito de limite infinito nos seguintes problemas:
 (resposta: -
(resposta: - )
)Primeiramente, abri a expressão e apliquei o limite trigonométrico fundamental:

Daí, apliquei as propriedades operatórias dos limites:
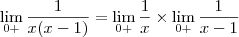
Resolvendo (acredito que o erro está aqui):
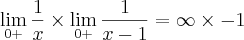 Seria muita inocência imaginar que infinito multiplicado por -1 daria
Seria muita inocência imaginar que infinito multiplicado por -1 daria  , que é a resposta?
, que é a resposta?O outro, se não se importarem:
 (resposta: 0)
(resposta: 0)Desenvolvi, rumo ao limite trigonométrico fundamental e multipliquei por x/x:
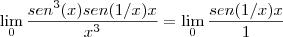
Daí, separando os limites temos que o limite de "x" é zero:
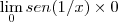
Novamente, seria muita inocência imaginar que infinito multiplicado por zero dá zero?
Ufa, agradeceria qualquer luz que algum amigo puder dar.



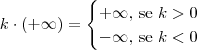 , sendo
, sendo 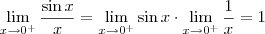 , mas
, mas  e
e 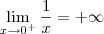 .
. , porém o resultado é 1.
, porém o resultado é 1.
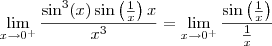

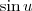 é uma função limitada e
é uma função limitada e 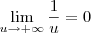 , então
, então 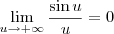 .
.

 .
.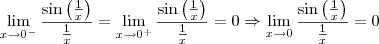


 , avisa que eu resolvo.
, avisa que eu resolvo.

