Galera, não consigo fazer essa questão de jeito nenhum, ve se alguem me da uma força abraços
(ITA - 1995) Considere C uma circunferência
centrada em O e raio 2r, e t a reta tangente a C num ponto T. Considere também A um ponto de C tal que AÔT =? é um ângulo agudo. Sendo B o ponto de t tal que o segmentoAB é paralelo ao segmento
OT, então a área do trapézio OABT é igual a:
(A) r²(2 cos? - cos 2?)
(B) 2r²(4 cos? - sen 2?)
(C) r²(4 sen? - sen 2?)
(D) r²(2 sen? + cos?)
(E) 2r²(2 sen 2? - cos 2?)


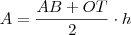 sendo h a altura do trapézio, sendo que OT = 2r.
sendo h a altura do trapézio, sendo que OT = 2r.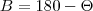 , para achar AK:
, para achar AK: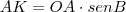

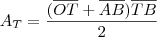 .
.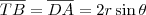 , usando o triângulo ODA.
, usando o triângulo ODA.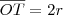 , falta determinar
, falta determinar  . Para isso, vamos aplicar o Teorema de Pitágoras no triângulos ODA (lembrando que
. Para isso, vamos aplicar o Teorema de Pitágoras no triângulos ODA (lembrando que  ).
).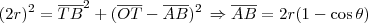 (fica como exercício desenvolver essa parte
(fica como exercício desenvolver essa parte  )
)}{2} = r^2(4-2\cos\theta)\sin\theta A_T = \frac{[2r + 2r(1-\cos\theta)](2r\sin\theta)}{2} = r^2(4-2\cos\theta)\sin\theta](/latexrender/pictures/be3b3ac1732a9c81eb074f1f5a297042.png)
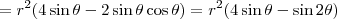

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)