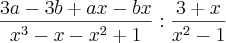
Fatorando cheguei até:
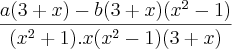
Até aí está certo? Como prossigo? O gabarito diz
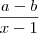
obrigado novamente

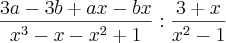
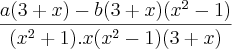
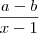


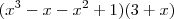 que equivale a
que equivale a 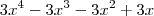 , para eu deduzir uma raiz eu faria
, para eu deduzir uma raiz eu faria 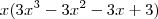 ,
,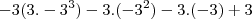 deu -42.
deu -42.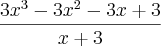

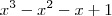 .
.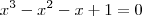
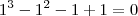
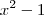 . Agora, obtendo as raízes de
. Agora, obtendo as raízes de 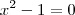 , nós teremos x'=1 e x''=-1.
, nós teremos x'=1 e x''=-1.![x^3-x^2-x+1 = (x-1)(x-1)[x-(-1)] = (x-1)^2(x+1) x^3-x^2-x+1 = (x-1)(x-1)[x-(-1)] = (x-1)^2(x+1)](/latexrender/pictures/c5784f486c1cf1f85e3c2f8a547bc0be.png)

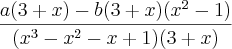 =
=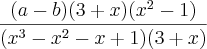 =
=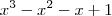 por (x-1) para reduzir o grau do polinômio
por (x-1) para reduzir o grau do polinômio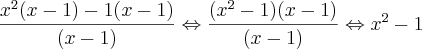
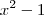 , achei as raízes 1 e -1, e já tenho a outra raíz 1 que usei para reduzir o grau do polinômio.
, achei as raízes 1 e -1, e já tenho a outra raíz 1 que usei para reduzir o grau do polinômio.
 (resposta do gabarito)
(resposta do gabarito) , para ver se seria igual a
, para ver se seria igual a 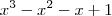 e não dá.
e não dá.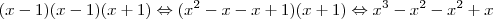 qual o meu erro? porque que essa multiplicação não está dando
qual o meu erro? porque que essa multiplicação não está dando 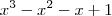 ????
????
lucas7 escreveu:Porém, eu fiz o teste e multipliquei (x-1)(x-1)(x+1), para ver se seria igual ae não dá.
qual o meu erro? porque que essa multiplicação não está dando
????
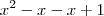 . Você apenas aplicou a distributiva multiplicando cada termo do fator
. Você apenas aplicou a distributiva multiplicando cada termo do fator 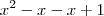 por x.
por x.
 passo a passo? Ao meu entendimento, que está errado, qualquer número multiplicado por 1 dá ele mesmo.
passo a passo? Ao meu entendimento, que está errado, qualquer número multiplicado por 1 dá ele mesmo.
lucas7 escreveu:Tem como você exemplificar? Ao meu entendimento, que está errado, qualquer número multiplicado por 1 dá ele mesmo.
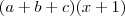 ?
?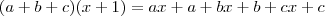

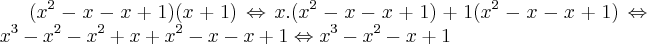

lucas7 escreveu:Entendi:
É isso professor?




Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)