 por Emilia » Ter Fev 15, 2011 23:19
por Emilia » Ter Fev 15, 2011 23:19
Segundo o IBGE, os recenseamentos feitos no Brasil nas
ultimas décadas fornecem os dados mostrados na tabela abaixo:
Ano População
1940 41.236.315
1950 51.944.397
1960 70.191.370
1970 93.139.037
1980 119.002.706
1990 146.352.150
2000 169.544.443
Então:
a) Calcule a taxa média anual de crescimento de 1940 a 2000.
b) A partir dos censos de 1990 e 2000, é possível fazer uma previsão de qual será a população no ano
2020? Qual seria esta população? Qual a taxa média de crescimento anual nesse período?
Resolva utilizando dois modelos: i) crescimento em PG, sendo o primeiro termo da PG em 1990 e o
termo 11º em 2000 e ii) supondo que o crescimento da população é dado por P=P0exp(Kt), onde
P=população, t=tempo em anos e k=constante a ser determinada.
c) Em algum momento os dois modelos citados no item anterior fornecerão a mesmo previsão quanto
a população do país?
d) Considerando a população do ano 2000, em quanto tempo, a partir deste ano, a população
duplicará? Qual seria a taxa média de crescimento anual desta população a partir do ano 2000?
Responda segundo cada modelo utilizado no item b.
e) Os modelos utilizados podem ser considerados realistas?
-
Emilia
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Ter Nov 30, 2010 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por rosimeire » Qua Fev 16, 2011 18:17
por rosimeire » Qua Fev 16, 2011 18:17
Eu consequi resolver a letra, a do exercício : média anual de crescimento de 1940 a 2000, vc deve somar toda a população e dividir por 7, que é a quantidade de população e ai vc obtera o resultado . Não tive tempo ainda de solucionar as outras respostas .gostaria de saber tb. ok!
-
rosimeire
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Fev 09, 2011 16:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: MATEMÁTICA
- Andamento: cursando
 por IRA_O_CARA » Sáb Fev 19, 2011 10:36
por IRA_O_CARA » Sáb Fev 19, 2011 10:36
EU CALCULEI A MÉDIA DA SEGUINTE FORMA:
(169544443-41236315)/60 = 5,186% por ano
Iraedson
-
IRA_O_CARA
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Fev 19, 2011 10:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: MATEMÁTICA
- Andamento: cursando
 por arima » Sáb Fev 19, 2011 12:36
por arima » Sáb Fev 19, 2011 12:36
Como ele quer a taxa logo será que não deva fazer a média geometrica? Também estou em duvida.
-
arima
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sáb Out 23, 2010 18:25
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por Emilia » Dom Fev 20, 2011 12:49
por Emilia » Dom Fev 20, 2011 12:49
Iraedson, depois que você dividiu por 60, como chegou na taxa de 5,18%?
-
Emilia
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Ter Nov 30, 2010 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por aguiarubra » Seg Fev 21, 2011 10:16
por aguiarubra » Seg Fev 21, 2011 10:16
Emília
Vamos considerar os seguintes cálculos preliminares (eu tenho uma calculadora "Ofi Calc" que obtive, gratuitamente, na web):
q = 169.544.443 - 41.236.315 = 2.138.468,79999999981
P = 41.236.315
i =
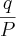
=
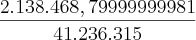
= 0,051858872453
i % = 0,051858872453 . 100 = 5,1858872453
Finalmente, arredondando 5,1858872453 para 5,186 chegamos ao valor 5,186 %
-
aguiarubra
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Fev 21, 2011 09:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Exponencial e Logaritmo
por solcruz » Sáb Mar 05, 2011 20:38
- 0 Respostas
- 2060 Exibições
- Última mensagem por solcruz

Sáb Mar 05, 2011 20:38
Trigonometria
-
- [Derivada de Logaritmo Natural] Exercício de logaritmo
por Ronaldobb » Dom Out 28, 2012 17:40
- 1 Respostas
- 2571 Exibições
- Última mensagem por MarceloFantini

Dom Out 28, 2012 18:16
Cálculo: Limites, Derivadas e Integrais
-
- [logaritmo]dúvida sobre logaritmo
por tigocma » Ter Mar 25, 2014 22:43
- 0 Respostas
- 1846 Exibições
- Última mensagem por tigocma

Ter Mar 25, 2014 22:43
Logaritmos
-
- [Função exponencial] Exercício sobre função exponencial
por fff » Ter Jan 07, 2014 17:51
- 3 Respostas
- 4072 Exibições
- Última mensagem por fff

Qua Jan 08, 2014 06:47
Funções
-
- Logaritmo
por JailsonJr » Sex Mai 21, 2010 05:11
- 3 Respostas
- 2729 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:33
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




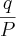 =
= 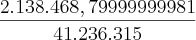 = 0,051858872453
= 0,051858872453