17)
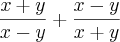 como que eu igualo esses denominadores? Eu não entendi como faz o mmc.
como que eu igualo esses denominadores? Eu não entendi como faz o mmc.Outro exemplo:
19)

Preciso de uma solução numa maneira bem explicativa, passo a passo, para eu poder entender.
Obrigado.

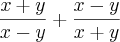 como que eu igualo esses denominadores? Eu não entendi como faz o mmc.
como que eu igualo esses denominadores? Eu não entendi como faz o mmc.

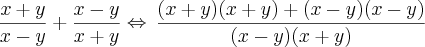
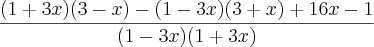 (Aqui o procedimento adotado é o mesmo do exercício 17)
(Aqui o procedimento adotado é o mesmo do exercício 17)
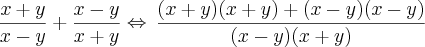

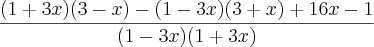 (Aqui o procedimento adotado é o mesmo do exercício 17)
(Aqui o procedimento adotado é o mesmo do exercício 17)
 =
= 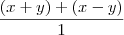 =
=  .... Segundo o gabarito seria
.... Segundo o gabarito seria 
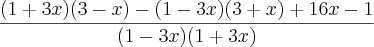 =
=  =
= 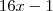
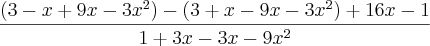 =
= 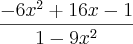
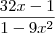

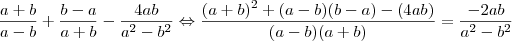




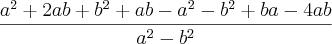
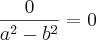


Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes