Boa noite, continuo na luta estudando esse assunto. Entrei nos exercícios de fatoração por agrupamento, e consegui resolver a maioria deles. Porém, dois deles eu não consegui chegar a resolução(talvez por algo errado ou talvez porque o exercício esteja incorreto), mas agradeceria muito se você, Renato, ou alguém, pudesse dar uma olhada para mim:
O primeiro,
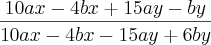
, tentei fatorar usando todos os possiveis fatores comuns entre eles.
O melhor que eu cheguei foi
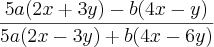
, segundo o livro pelo qual estou estudando, o resultado deveria ser:

.
E além desse, o outro que eu não consegui resolver mas cheguei perto também foi:

.
Na parte dos numeradores, eu consegui fatorar da seguinte forma mas embaixo não deu certo:
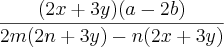
O resultado, segundo o livro:

E como eu consegui isolar esse (a-2b) nos numeradores, eu sinto que cheguei perto, mas não sei o que há de errado, o exercício e o gabarito não condizem? Ou tem alguma resolução?
Esses são os únicos dois que faltaram, e após isso entrarei em soma e subtração, multiplicação e divisão de frações algébricas. Muito obrigado.
ps: Sobre a outra questão, aquela que você deduziu o 24 no lugar de 2y, ficando

consegui resolvê-la, aprendi um método de usar a fórmula de bháskara, e usar as raizes para formar a multiplicação e deu várias questões. Naquela, particularmente, pelo denominador não possuir o "b", a bhaskara deu 2, e ficou 6(x+2)(x+2), quando a multiplicação certa para chegar ao 6x^2-24 seria 6(x-2)(x+2), então talvez a bhaskára só possa ser utilizada para obter as raízes da fórmula a.(x-r1).(x-r2) quando se possui a, b e c diferente de zero? Bom, agradeço novamente a ajuda naquela questão. E espero que tenham paciência com minhas perguntas, sei que são meio básicas comparadas a de muita gente aqui. Obrigado.
O gênio, esse poder que deslumbra os olhos humanos, não é outra coisa senão a perseverança bem disfarçada.
Johann Goethe

 , e no gabarito a resposta é
, e no gabarito a resposta é 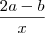



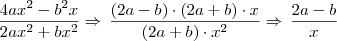





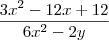
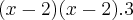 e o denominador o melhor que consegui foi
e o denominador o melhor que consegui foi  , porém não adianta para fatorar. O resultado dessa questão é
, porém não adianta para fatorar. O resultado dessa questão é  .
.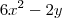 seria
seria  , pois aí você teria o resultado idêntico ao do gabarito, pois:
, pois aí você teria o resultado idêntico ao do gabarito, pois:![6x^2 - 24 \Rightarrow \, 3 \cdot [ 2 \cdot (x+2) \cdot (x-2) ] 6x^2 - 24 \Rightarrow \, 3 \cdot [ 2 \cdot (x+2) \cdot (x-2) ]](/latexrender/pictures/a326871baa7c0cc5f52e1f5994ad5e81.png)
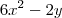 mesmo no denominador. Fiz questão de checar pois uma das questões anteriores eu tinha repassado errado. A questão deve ter sido digitada incorretamente no livro, porque estava indo bem na matéria depois da sua ajuda, mas essa aí tinha me travado de novo. Impressionante você saber o o valor que teria que ser para dar o resultado do gabarito. Obrigado mais uma vez Renato!
mesmo no denominador. Fiz questão de checar pois uma das questões anteriores eu tinha repassado errado. A questão deve ter sido digitada incorretamente no livro, porque estava indo bem na matéria depois da sua ajuda, mas essa aí tinha me travado de novo. Impressionante você saber o o valor que teria que ser para dar o resultado do gabarito. Obrigado mais uma vez Renato!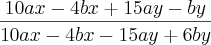 , tentei fatorar usando todos os possiveis fatores comuns entre eles.
, tentei fatorar usando todos os possiveis fatores comuns entre eles. 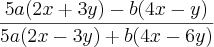 , segundo o livro pelo qual estou estudando, o resultado deveria ser:
, segundo o livro pelo qual estou estudando, o resultado deveria ser: .
. .
.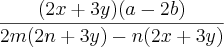

 consegui resolvê-la, aprendi um método de usar a fórmula de bháskara, e usar as raizes para formar a multiplicação e deu várias questões. Naquela, particularmente, pelo denominador não possuir o "b", a bhaskara deu 2, e ficou 6(x+2)(x+2), quando a multiplicação certa para chegar ao 6x^2-24 seria 6(x-2)(x+2), então talvez a bhaskára só possa ser utilizada para obter as raízes da fórmula a.(x-r1).(x-r2) quando se possui a, b e c diferente de zero? Bom, agradeço novamente a ajuda naquela questão. E espero que tenham paciência com minhas perguntas, sei que são meio básicas comparadas a de muita gente aqui. Obrigado.
consegui resolvê-la, aprendi um método de usar a fórmula de bháskara, e usar as raizes para formar a multiplicação e deu várias questões. Naquela, particularmente, pelo denominador não possuir o "b", a bhaskara deu 2, e ficou 6(x+2)(x+2), quando a multiplicação certa para chegar ao 6x^2-24 seria 6(x-2)(x+2), então talvez a bhaskára só possa ser utilizada para obter as raízes da fórmula a.(x-r1).(x-r2) quando se possui a, b e c diferente de zero? Bom, agradeço novamente a ajuda naquela questão. E espero que tenham paciência com minhas perguntas, sei que são meio básicas comparadas a de muita gente aqui. Obrigado.


 para
para  :
: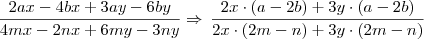

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)