A anlisando o código LaTeX que você escreveu, acredito que você estava querendo dizer:
Na sua mensagem original, você escreveu o seguinte comando:
q\prec-\frac{187}{13}\precq+1
Note que você escreveu
\precq ao invés de
\prec q.
Além disso, você deve usar o símbolo < e não

nesse caso.
Agora vamos a solução.
Note que -187/13 é aproximadamente
-14,385.
Esse número deve estar entre dois inteiros consecutivos (isto é, entre
q e
q+1). Portanto, devemos ter que
q = -15.
Se quiser fazer de outra forma, você deve resolver duas inequações:
(a) q < -187/13
Sabemos que -187/13 é aproximadamente
-14,385, então temos que
q < -14,385.
(b) -187/13 < q + 1
(-187/13) - 1< q
(-187 - 13)/13 < q
-200/13 < q
Sabemos que -200/13 é aproximadamente -15,385, então temos que
-15,385 < q.
Juntando as soluções de (a) e (b), então temos que:
-15,385 < q < -14,385Como q é inteiro, então o único valor que atende a essa inequação é -15.


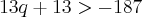




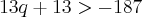





 nesse caso.
nesse caso.




 , avisa que eu resolvo.
, avisa que eu resolvo.

